9. Sınıf Matematik Ders Kitabı Cevapları MEB Yayınları 2021-2022
12.09.2023 - 15:29 | Son Güncellenme:
Eğitim öğretim hayatında öğrencilerin en çok karşısına çıkan derslerden birisi de matematiktir. İlkokul döneminde başlayan matematik dersleri üniversite dönemine kadar sürmektedir. Özellikle LGS, YKS oturumları TYT-AYT ve memur sınavları gibi KPSS'de öğrencilerin ihtiyaç duyduğu alanlardan bir tanesidir. Matematik ders konuları MEB tarafından açıklanan müfredata göre düzenlenmektedir. 9. sınıf matematik ders kitabında öğrencilerin kendisini geliştirmesi için çeşitli örnekler ve etkinlikler yer almaktadır. 2021-2022 yılında 9. sınıf matematik ders kitabı cevapları MEB yayınlarını öğrenmek istiyorsanız içeriğimize göz atabilirsiniz.

Matematik dersi öğrencilerin eğitim öğretim hayatında en sık karşılaştığı alanlardandır. Özellikle lise geçiş, üniversite giriş ve memur alımı gibi çeşitli merkezi sınavlarda öğrenciler matematiğe ihtiyaç duymaktadır. Matematik ders konuları MEB tarafından her yıl açıklanan müfredata göre düzenlenir. 9 sınıf matematik ders kitabında kümelerden mantığa kadar pek çok konu işlenmiştir.
9. Sınıf Matematik Ders Kitabı Sayfa 18 Cevapları
1. Aşağıdaki ifadelerin birer önerme olup olmadığını yanındaki boşluklara yazınız.
a) Birbirinden farklı en küçük üç asal sayının toplamı 10 dur. (2+3+5=10 Önermedir)
b) Türkiye Cumhuriyeti Asya kıtasındadır. (Önerme)
c) Fatih bu okulda mı? (Önerme değil)
ç) Ay Dünya’nın uydusudur. (Önerme)
d) Bugün hava güzel mi? (Önerme değil)
2. Aşağıdaki önermelerin doğruluk değerlerini yandaki boşluklara yazınız.
a) ‘‘6 + 3 > 7 dir.’’ (1)
b) ‘‘En büyük iki negatif tam sayının toplamı -2 dir.’’ (0)
c) ‘‘Dünyada ilk kalorifer sistemi İshakpaşa Sarayı’nda kullanılmıştır.’’ (1)
ç) ‘‘10 ile 19 arasında 8 sayı vardır.’’ (1)
d) ‘‘2 sayısı, 2x – 3 = 1 denkleminin çözüm kümesinin bir elemanıdır.’’ (1)
3. Aşağıdaki önermelerden hangilerinin birbirine denk önerme olduğunu bulunuz.
a) p: ‘‘Mardin ili, Güney Doğu Anadolu Bölgesi’ndedir.’’ (1)
b) q: ’’32 – 22 < (-2)2 dir.’’ (0)
c) r: ‘‘Negatif asal sayı yoktur.’’ (1)
ç) s: (-2)2 . (-1)101 / (-3)2 + (-5) > 0'dır (0)
p denktir r'ye
q denktir s'ye
4. Aşağıdaki önermelerin olumsuzlarını yazınız.
a) p: ‘‘Fındık üretiminde Türkiye dünya birincisidir. (p' Fındık üretiminde Türkiye dünya birincisi değildir)
b) q: ‘‘3x+5>-2 ifadesini sağlayan en küçük x tam sayı değeri -3 tür.’’ (q' 3x+5<=-2 ifadesini sağlayan en küçük x tam sayı değeri -3 değildir)
c) r: 1/2 + 1/4 : 1/2 = 1'dir (r' 1/2 + 1/4 : 1/2 # 1'dir)
5. 7 farklı önermenin birbirine göre kaç tane doğruluk durumu olacağını bulunuz.
2^7=128
7 farklı önermenin birbirlerine göre 128 tane doğruluk durumu vardır.
6. n+2 tane farklı önermenin birbirine göre 64 farklı doğruluk durumu olduğuna göre n sayısını bulunuz.
2 ^ (n + 2) = 64
n + 2 = 6
n = 4
6 önerme birbirine göre 64 farklı doğruluk değerine sahip olur.
9. Sınıf Matematik Ders Kitabı Sayfa 28 Cevapları
1. p: ‘‘İki basamaklı en küçük tam sayı -99 dur.’’ (1)
q: ‘‘Camın ham maddelerinden biri kumdur.’’(1)
r: ‘‘Bir asal sayının 2 katının 1 fazlası daima bir asal sayıdır.’’ (0)
7 X 2 + 1 = 15 Asal değildir. Bu örnekle aksini kanıtladığınız için bu önerme doğru değildir.
önermelerine göre aşağıdaki bileşik önermelerin doğruluk değerlerini bulunuz.
a) (p V q') Λ r
= ( 1 V 1') Λ 0
= 1 Λ 0
= 0
b) (p Λ q)' V r
= (1 Λ 1)' V 0
= 1' V 0
= 0 V 0
= 0
c) (p' V r) V (p Λ q')'
= (0' V 0) V ( 0 Λ 1')'
= (1 V 0) V ( 0 Λ 0)'
= 1 V 0'
= 1 V 1
= 1
ç) p Λ (q Λ r')
= 1 Λ (1 Λ 0')
= 1 Λ (1 Λ 1)
= 1 Λ 1
= 1
2. Aşağıdaki ifadelerin doğruluk değerini bulunuz.
a) (1 V 0) Λ 1 = 1 Λ 1 = 1
b) (0 Λ 1) V (1 V 0)' = 0 V 1' = 0 V 0 = 0
c) (1' Λ 0) V (0 V 1) = (0 Λ 0) V 1 = 0 V 1 = 1
ç) (1 Λ ((1 Λ 1) Λ 1) Λ 1') = (1 Λ (1 Λ 1) Λ 0) = 1 Λ 1 Λ 0 = 0
3. Aşağıdaki denkliklerden doğru olanın yanına (D), yanlış olanın yanına (Y) yazınız.
a) p' V p ≡ 1 (D)
b) (p Λ q')' ≡ p' V q (D)
c) p Λ (q V r) ≡ (p V q) Λ (p V r) (Y)
ç) p Λ 1 ≡ 1 (Y)
4. Aşağıdaki bileşik önermelerin en sade şeklini bulunuz.
a) p V (p Λ q)' ≡ p V (p' V q') ≡ (p V p') V q' ≡ 1 V q' ≡ 1
b) (p V q')' Λ p ≡ (p' Λ q) Λ p ≡ (p' Λ p) Λ q ≡ 0 Λ q ≡ 0
c) (p V q') Λ (p' Λ q)' ≡ (p V q') Λ (p V q') ≡ p V ( q' Λ q') ≡ p V q'
ç) (p V q')' V (p' Λ q') ≡ (p' Λ q) V (p' Λ q') ≡ p' Λ (q' V q) ≡ p' Λ 1 ≡ p'
5. (p V q')' Λ (q Λ r) ≡ 1 olduğuna göre p, q ve r önermelerinin doğruluk değerlerini bulunuz.
p V q')'≡ 1
(q Λ r) ≡ 1 ( burada ve olduğu için her iki tarafta bir olmak zorundadır.
q ≡ 1 , r ≡ 1 bulunur.
(p V q')'≡ 1 olmalı değili 1 ise kendisi 0 olur.
p V q' ≡ 0
q≡1 idi değili 0 yapar ;
p V 0 ≡0 ise ; p≡0 bulunur.
Doğruluk değerleri ;
p ≡ 0 , q ≡ 1 , r ≡ 1 bulunur.
6. Aşağıdaki ifadelerin en sade şeklini bulunuz.
a) (p Λ 0) V (p V 1)
(p Λ 0) V (p V 1) burada, (p V 1 ) her zaman 1 dir doğrudur dolayısıyla (P V 1)'i dikkate almayabiliriz
(p Λ 0) V 1 Veya bağlacında bir taraf doğruysa diğer tarafta ne olursa olsun ifade doğrudur.
Sonuç "1" bulunur.
b) (p V 0) Λ (p' Λ 1)
(p V 0) Λ (p' Λ 1) burada p önermesi ya 1 dir ya 0 dır.
Birinci olasılık; p = 1 için p' = 0;
(1 v 0 ) = 1, (0 Λ 1)= 0 , 1 Λ 0 = 0 bulunur.
İkinci olasılık; p = 0 için p' = 1;
( 0 V 0 ) = 0, ( 1 Λ 1 ) = 1, 0 Λ 1 = 0 bulunur .
Sonuç "0" bulunur.
7. 19 Mayıs Lisesinde görev yapan Müdür Yardımcısı Selin Hanım, nöbetçi öğrenciyi çağırarak 9-C sınıfından Kemal veya Yağmur’un odasına gelmesini söylemiştir. Nöbetçi öğrenci 9-C sınıfına girerken çağrılan iki öğrenci için arada kullanılan “ veya” bağlacını unutmuştur. Buna göre,
a) Nöbetçi öğrenci bağlacı “ve” olarak hatırlarsa hangi olası durumların gerçekleşeceğini bulunuz.
b) Nöbetçi öğrenci bağlacı “ya da” olarak hatırlarsa hangi olası durumların gerçekleşeceğini bulunuz.
c) Nöbetçi öğrenci Selin Hanım’ın söylediğini doğru hatırlarsa hangi olası durumların gerçekleşeceğini bulunuz.
a) Bağlaç "ve" olarak kabul edilirse hem Yağmur hem de Kemal müdürün odasına çağrılır.
b) Bağlaç "ya da" olarak kabul edilirse ya Yağmur ya da Kemal müdürün odasına çağrılır. Yani ikisinden yalnızca biri.
c) Bağlaç "veya" olarak kabul edilirse b şıkkındaki durum gerçekleşir. Yani müdürün odasına ya Yağmur ya da Kemal çağrılır.
8. (1 V 1') V (0 V 0') bileşik önermesinin doğruluk değerini bulunuz.
Çözüm :
(1 V 1') V (0 V 0') ≡ (1 V 0) V (0 V 1) ≡ 1 V 1 ≡ 1
9. (p' V q') V (p Λ q) bileşik önermesini en sade biçimde yazınız.
Çözüm :
(p' V q') V (p Λ q) ≡ (p Λ q)' V (p Λ q) ≡ p Λ (q V q') ≡ p Λ 1 ≡ p
9. Sınıf Matematik Ders Kitabı Sayfa 35 Cevapları
1. p ≡ 1, q ≡ 0, r ≡ 1 doğruluk değerlerine göre aşağıdaki bileşik önermelerin doğruluk değerlerini bulunuz.
a) p ⇒ (q Λ r) = 1 ⇒ (0 Λ 1) ≡ 1 ⇒ 0≡ 0
b) (p V q) ⇒ r = (1 V 0) ⇒ 1 ≡ 1 ⇒ 1 ≡ 1
c) (p ⇒ q) ⇒ (q ⇒ r) = (1 ⇒ 0) ⇒ (0 ⇒ 1) ≡ 0 ⇒ 1 ≡ 1
ç) (q' ⇒ p) ⇒ r' = (1 ⇒ 1) ⇒ 0 ≡ 0 ⇒ 0 ≡ 0
2. (p Λ q') ⇒ r ≡ 0 ise (p ⇒ r)' ⇒ (q V r') bileşik önermesinin doğruluk değerini bulunuz.
(p Λ q') ⇒ r ≡ 0 önermesi ise bağlacının özelliğinden yararlanarak hareket edersek burada doğrudan yanlışa ulaştığımız zaman doğruluk değeri "0"'dır yani yanlıştır, dolayısıyla (p Λ q') ifadesi doğrudur yani 1, r ifadesi 0'dır.
(p ⇒ r)' ⇒ (q V r') parantez içini çözelim;
(p' V q )' = ((p')' Λ q' ) = (p Λ q' ) ifadesine 1,
1 ⇒ (q V r') burada r ifadesine 0 değili ise 1 olacaktır,
1 ⇒ (q V 1) ifadesi, (q V 1) her zaman 1 olur,
1 ⇒ 1 ifadesi doğrudan doğruya ulaşırsak sonuç doğrudur
Doğruluk değeri 1'dir.
3. (p' ⇒ q)' ⇒ p' bileşik önermesini en sade biçimde yazınız.
(p ⇒ q)' V (p ⇒ q)
p' ⇒ q ≡ p V q
(p' ⇒ q)' ⇒ q' ≡ (p V q)' ⇒ p'
≡ (p V q)' ⇒ p' iki bağlaç aynı birleştirelim
≡ (p V p') ⇒ q
≡ 1 V q
≡ 1
4. (p ⇒ q)' V (p ⇒ q) bileşik önermesini en sade biçimde yazınız.
p ⇒ q ≡ X diyelim öyleyse ifade
X V X' ≡ 1 olur
5. (p ⇒ q')' V (q ⇒ p)' bileşik önermesini en sade biçimde yazınız.
(p ⇒ q')' V (q ⇒ p)'
(p V q)' V (p' V q)
(p Λ q') V (p' V q)
(p Λ q') V (p' Λ q)'
1 V 0
1
6. ‘‘Bayrak dalgalanırsa vatan düşmez.’’ önermesinin tersini, karşıtını ve karşıt tersini yazınız.
Tersi - Bayrak dalgalanmazsa vatan düşer.
Karşıtı - Vatan düşerse, bayrak dalgalanmaz.
Karşıt tersi - Vatan düşmezse, bayrak dalgalanır.
Karşıt durumda, ikinci cümle ile birinci cümle yer değiştirir. Terste ise olumsuzu alınır. Karşıt terste ise hem olumsuzu alınır, hem de yer değişimi yapılır.
7. (p ⇔ q) Λ (q Λ p') bileşik önermesini en sade biçimde yazınız.
(p ⇒ q ) Λ (q ⇒ p ) Λ (q Λ p')
( p' V q) Λ (q' V p) Λ (q Λ p')
( p' V q) Λ (q Λ p') Λ (q' V p)
( p' V q) ≡ (p Λ q' )'
(q' V p) ≡ (q Λ p' ) '
(p Λ q' )' Λ (q Λ p') Λ (q Λ p' )'
(q Λ p') Λ (q Λ p' )'
(q Λ p') ve (q Λ p' )' önermeleri var ve bu iki önerme "ve" bağlacıyla bağlanmış. İki önermeden birisi diğerinin değilidir. Dolayısıyla 0'dır. Ve bağlacıyla bağlandığı için bileşik önermenin en sade biçimi 0'dır.
8. 30 kişilik bir sınıfta Pınar, Remzi, Kaan ve Nilgün dışındaki öğrencilerin devamsızlık yapmadığı bilinmektedir. Matematik öğretmeni Gülendam Hanım, bu öğrenciler için aşağıdaki tablodaki sembolik mantık kurallarını belirlemiştir.
Sınıfta ise Sınıfta değil ise
Pınar p (0) p' (1)
Remzi r (1) r' (0)
Kaan k (1) k' (0)
Nilgün n (1) n' (0)
Gülendam Hanım bu sınıfa derse girdiğinde yoklama sonucunu tahtaya sembolik mantık kurallarını kullanarak aşağıdaki şekilde yazmıştır:
I) p' Λ r ≡ 1 (r ≡ 1 p ≡ 0)
II) k ⇒ p ≡ 0 (k ≡ 1 p ≡ 0)
III) p' ⊻ n ≡ 0(1 V n ≡ 0 ⇒ n ≡ 1)
Yukarıda verilen denkliklere göre
a) Pınar, Remzi, Kaan ve Nilgün arasından sınıfta olanları bulunuz. (Remzi, Kaan, Nilgün)
b) Sınıfta var olan öğrenci sayısını bulunuz. (üç tane)
c) “Kaan sınıfta ise Pınar sınıfta değildir.” önermesinin doğruluk değerini bulunuz. (1 ⇒ 1 ≡ 1)
9. Sınıf Matematik Ders Kitabı Sayfa 39-40 Cevapları
1. Aşağıdaki ifadelerden hangisi önerme değildir?
A) Merkür kızıl gezegen adıyla bilinir.
B) Türkiye yedi coğrafi bölgeye ayrılmıştır.
C) Hadi ders çalışalım.
D) Dünya Savaşı İttifak Devletleri’nden birisi Alman İmparatorluğu’dur.
E) 3 bir rasyonel sayıdır.
Ünlem, soru vb. ifadeler önermeler olmaz. Çünkü ya doğru ya yanlış diyemeyiz. Ortada net bir şey yok.
2. Aşağıdaki önermelerden hangisinin olumsuzunun doğruluk değeri ‘‘1’’ dir?
A) Ankara Türkiye’nin başkentidir.
B) İki basamaklı 45 tane çift sayı vardır.
C) Üçgenlerin iç açıları toplamı 180 derecedir.
D) Tavşan uçan bir hayvandır.
E) Basketbol maçlarında her takım 5 oyuncu ile sahada mücadele eder.
3. p: ‘‘Fatih Sultan Mehmet İstanbul’u fethetti.’’ q: ‘‘İstanbul’un Fethi Orta Çağ’ı kapattı.” önermeleri kullanılarak aşağıdaki denklikler oluşturulmuştur.
p / q / 1
(p' 0 q) / q' / 0
III. (p 0 q)' / 0
(p / q')' 0 p' / 0
Yukarıdaki denkliklerden hangileri doğrudur?
A) I – III B) II – IIl C) I – ll – III D) ll – III-IV E) I- II – IV
4. (p V q') Λ (p V q) bileşik önermesinin en sade hâli aşağıdakilerden hangisidir?
A) p B) pl C) q D) ql E) 1
Çözüm:
(p V q') Λ (p V q) ≡ p V (q Λ q') ≡ p V 0 ≡ p
5. [p V (p' Λ q)] Λ (p' Λ q') önermesi aşağıdakilerden hangisine denktir?
A) p 0 p' B) 0 C) p / q' D) p E) 1
Çözüm:
[p V (p' Λ q)] Λ (p' Λ q')
(p V p') Λ (p V q) Λ (p' Λ q')
1 Λ (p V q) Λ (p V q)' // (p Λ q) = x diyelim
1 Λ (X Λ X')
1 Λ 0
0
6. p => (q V r) ≡ 0 olduğuna göre (p' => q) => (q' => r') önermesi aşağıdakilerden hangisine denktir?
A) p B) q C) q' D) 1 E) p'
Çözüm:
1 => 0 ≡ 0
p ≡ 1 q V r ≡ 0
p ≡ 1 q ≡ 0 r ≡ 0
(p' => q) => (q' => r')
(0 => 0) => (1 => 1)
1 => 1
1
7. (p => q) Λ (q' => p) bileşik önermesinin en sade hâli aşağıdakilerden hangisidir?
A) p B) q C) 1 D) q' E) p'
Çözüm:
p => q ≡ p' V q özellik
(p => q) Λ (q' => p)
(p' V q) Λ (q V p)
(p' V q) Λ (p V q) // Dağılma özelliği
(p' Λ p) V q
0 V q
q
8. p: ‘‘Beyazla siyah zıt renklerdir.’’
q: ‘‘111 sayısı bir asal sayıdır.’’
r: ‘‘Balıklar suda yaşar.’’
Önermeleri kullanılarak aşağıdaki bileşik önermelerin doğruluk değerleri bulunmuştur.
(p => q) Λ r ≡ 0 // (1 => 0) Λ 1 ≡ 0 Λ 1 ≡ 0 (D)
(p => q') V r' ≡ 0 // (1 =>1) V 0 ≡ 1 V 0 ≡ 1 (Y)
III. (q => p) => (r => p') ≡ 1 // (0 => 1) => (1 => 0) ≡ 1 => 0 ≡ 0 (Y)
(p V q') => (p Λ r) / 1 // (1 V 1) => (1 Λ 1) ≡ 1 => 1 ≡ 1 (D)
Yukarıdaki denkliklerden hangileri doğrudur?
A) I – III B) I – IV C) II – III D) II – IV E) I – III – IV
9. ‘‘ Toplum duyarlı olursa engellilere engel kalmaz.’’ önermesinin olumsuzu aşağıdakilerden hangisidir?
A) ‘‘Toplum duyarlı olmaz ise engellilere engel kalmaz.’’
B) ‘‘Toplum duyarlı olursa engellilere engel kalır.’’
C) ‘‘Toplum duyarlı olmazsa engellilere engel kalır.’’
D) ‘‘ Toplum duyarlı olur ve engellilere engel kalır.’’
E) ‘‘Toplum duyarlı olur veya engellilere engel kalmaz.’’
p = Toplum suyarlı olur
q = Engellilere engel kalır
p => q' ≡ p' V q
(p => q)' ≡ p V q'
Toplum duyarlı olur ve engellilere engel kalır.
10. Matematik öğretmeni İhsan Bey, Beyhan’ı tahtaya kaldırarak `p => (q Λ p') önermesinin olumsuzunu en sade biçime getirmesini istiyor. Beyhan çözüm için aşağıdaki adımları izliyor.
I. [p => (q Λ p')]' ≡ p' V (q Λ p')' (özellik)
II. ≡ p' V (q' V (p')') (D)
III. ≡ p' V (q' V p) (D)
IV. ≡ (p' V p) V q' (D)
V. ≡ q' (1 olması gerekiyor Y)
Beyhan kaçıncı adımda hata yapmıştır?
A) I B) II C) III D) IV E) V
a ≡ 0
b ≡ 1
x ≡ 0
y ≡ 1
11. Tabloda verilenlere göre aşağıdaki denkliklerden hangileri doğrudur?
I. a ⇔ b ≡ 1 / (0 ⇔ 1 ≡ 0)
II. x ⇔ y ≡ 0 / (0 ⇔ 1 ≡ 0)
III. a ⇔ x ≡ 1 / (0 ⇔ 0 ≡ 1)
IV. b ⇒ y ≡ 0 / (1 ⇒ 1 ≡ 1)
A) I-II B) II-III C) III-IV D) II-IV E) I-IV
12.
(D) I. p ⇔ p' / 0 | 0 ⇔ 1 ≡ 0 1 ⇔ 1 ≡ 0
(D) II. (p ⇔ q)' ≡ p' ⇔ q | Özellik
(Y) III. p ⇔ q ≡ (p ⇒ q) V (q ⇒ p) | p ⇔ q ≡ (p ⇒ q) Λ (q ⇒ p)
(D) IV. p ⇔ 1 ≡ p | 1 ⇔ 1 ≡ 1 0 ⇔ 1 ≡ 1
Yukarıdaki denkliklerden hangileri doğrudur?
A) I-Il B) I-IIl C) lI-IV D) I-II-lll E) I-II-IV
13. p: ‘‘x=2’’
q: ‘‘x2-4=0’’
r: ‘‘x=-2’’
önermeleri veriliyor.
I. (p & q) / (q & r)
II. (p 0 r) & q
III. q & (p 0 r)
IV. q + (p 0 r)
Yukarıdaki bileşik önermelerden hangilerinin doğruluk değeri ‘‘1’’ dir?
A) I-II-IV B) I-II-II C) II-III-IV D) I-III E) I-III-IV
14. I. p ⇔ (p ⇔ 0)
II. p ∨ (p ⇒ q)
III. (p ∨ q’) ∧ (p ∨ q’)’
IV. q’ ∨ (p ⇒ q)
Yukarıda verilen önermelerin kaç tanesinin doğruluk değeri 1 dir?
Cevap: D
15. I. “∀x ∈ Z, x4 +1 > 0”
II. “∃x ∈ Z, 5x – 4 = 16”
III. “∀x ∈ N, 3x – 1 = 2”
IV. “∃x ∈ Z, 4x2 + 3 < 0”
Yukarıda verilen önermelerin kaç tanesinin doğruluk değeri 0 dır?
A) 0
B) 1
C) 2
D) 3
E) 4
16. I. p (x): “∃x ∈ N, 3x – 4 > 0” ⇒ p’ (x):“∀x ∈ N, 3x – 4 < 0”
II. q (x):“∀x ∈ Z, 5x – 4 = 16” ⇒ q’ (x):“∃x ∈ Z, 5x – 4 ≠ 16”
III. r (x): “∃x ∈ Z, 7x + 3 < 1 ” ⇒ r’ (x):“∀x ∈ Z, 7x + 3 > 1 ”
Yukarıdakilerden hangisi ya da hangileri doğrudur?
A) Yalnız I
B) Yalnız II
C) I-II
D) I-III
E) II-III
17. (p ∧ q’) ⇒ q’ teoreminin hipotezi a önermesi, hükmü b önermesi olduğuna göre a’ v b ifadesine karşılık gelen değer aşağıdakilerden hangisidir?
A) p
B) p’
C) q
D) q’
E) 1
9. Sınıf Matematik Ders Kitabı Sayfa 45 Cevapları
1. Aşağıdakilerden hangisinin bir küme belirttiğini bulunuz.
a) Ankara’nın bazı ilçeleri (iyi tanımlanmamış)
b) Akif Palalı Lisesi öğretmenleri (Net olarak bellidir)
c) Okulumuzdaki bazı zayıf öğrenciler (Hangi öğrenciler olduğu net bir şekilde belirtilmemiş)
ç) Ülkemizdeki matematik profesörlerinden üçü (Hangi üçü net değil)
2. A = {a, b, c, {d, e}} kümesi için
(D) I. a ∈ A
(D) II. s{A} = 4
(Y) III. d ∈ A (Çünkü {d,e} bir bütün olarak eleman, burada d'yi ayıramayız)
(D) IV. {d, e} ∈ A
bilgilerinden hangilerinin doğru olduğunu bulunuz.
3. ‘‘HAKKARİ’’ sözcüğündeki harfleri H kümesi adıyla liste ve Venn şeması yöntemi ile gösteriniz.
Çözüm:
H= {H, A, K, R, İ}
4. Aşağıdaki kümelerin yanına sonlu küme ya da sonsuz küme kavramlarından uygun olanı yazınız.
a) A = {x | x2 < 16, x tam sayı} (sonlu, çünkü karesi 16'dan küçük olan sayılar sayılabilir.)
b) B = {x | x, 100 den küçük asal sayılar} (sonlu, çünkü 100'den küçük sayılar sayılabilir. )
c) C = {x | x, en az iki basamaklı doğal sayılar} (sonsuz, sayılamaz, {10, 11 ... 100, 1000 ....})
ç) D = {x | x, 3 ün veya 5 in katı olan tam sayılar} (sonsuz, {..., -5, -3, 0, 3, 6, 10, 15 ,,,})
5. Aşağıdakilerden hangileri boş küme belirttiğini bulunuz.
a) A = {a | -3 < a < 2, a bir asal sayı} (Boş Küme)
b) B = {x | x, haftanın p veya c harfi ile başlayan günleri} (Boş Değil) {pazar, pazartesi, salı}
c) C = {O} (Boş Değil, bu kümede boş küme elemanı burada bir eleman sayılır.)
ç) D = {x | x, karesi 3 olan rakamlar} (Boş Küme, çünkü rakamların hi. birinin karesi 3 olamaz)
9. Sınıf Matematik Ders Kitabı Sayfa 50 Cevapları
A = {a, b, c, {d}} kümesi için
I. d ∈ A
II. {a} ∈ A
III. {b} ⊊ A
IV. {c}, {d} ∈ A
bilgileri veriliyor. Buna göre yukarıdaki ifadelerden hangilerinin doğru olduğunu bulunuz.
Yalnız IV doğrudur.
2. Alt kümelerinin sayısı ile kendisi hariç alt kümelerinin sayısının toplamı 63 olan kümenin kaç elemanlı olduğunu bulunuz.
Çözüm:
2n + 2n -1 = 63
2n= 64
2n = 32 = 25
n = 5
3. A = {a, b, c, d, e} kümesinin alt kümelerinin kaç tanesinde;
a ve b nin eleman olarak bulunduğunu,
a veya b nin eleman olarak bulunduğunu,
III. a ve b den yanlız birinin eleman olarak bulunduğunu,
a elemanının bulunup, b elemanının bulunmadığını,
En çok bir sesli harfin bulunduğunu hesaplayınız.

4. C = {a, b, c, ç, d, e} kümesinin alt kümelerinin kaç tanesinde en az bir sesli harfin bulunabileceğini bulunuz.
Çözüm:
Tüm alt küme = 26 = 64
Sesli harfin olmadığı = 24 = 16
En az bir sesli harf 64 - 16 = 48
5. D = {x | -2 ≤ x < 9, x = 2n ve n ∈ Z } kümesinin alt küme sayısını bulunuz.
Çözüm:
D= {2, 0, 2, 4, 6, 8} s(B) = 6 26 = 64
6. A = {1, 2} ve B = {1, 2, 3, 4, 5} kümeleri veriliyor. A 3 K 3 B olmak koşulu ile
a) Kaç farklı K kümesinin yazılabileceğini, 23= 8
b) A dan farklı kaç tane K kümesinin yazılabileceğini, 8 - 1 = 7
c) A ve B den farklı kaç tane K kümesinin yazılabileceğini hesaplayınız. 8 - 2 = 6
9. Sınıf Matematik Ders Kitabı Sayfa 51 Cevapları
1.
A = {1, 3, 5}
B = {x | x, ANKARA kelimesindeki harfler} = {A, N, K, R}
C = {x | x, 7 den küçük tek sayma sayıları} = {5, 3, 1}
D = {C, A, N, K, R}
kümeleri veriliyor. Bu kümelerle ilgili;
l. A = C ll. A = D lll. A ≠ B lV. B = C
ifadelerinden hangilerinin doğru olduğunu bulunuz.
2. Aşağıdaki ifadelerin sonlarındaki boşluğa doğru olanlar için “D” yanlış olanlar için “Y” yazınız.
a) Eleman sayıları aynı olan kümelere eşit kümeler denir.(Y)
b) Eşit kümelerden biri diğerini kapsar. (D)
c) A M B ise A ! B dir. (D)
ç) Alt küme sayıları eşit olan kümeler daima eşit kümelerdir. (Y)
d) A 3 B ve A 4 B ise A = B dir. (D)
3. s(A) = 3 + x ve s(B) = 15 - 2x olarak verilen A ve B kümeleri eşit kümeler ise x in değerini bulunuz.
Çözüm:
3 + x = 15 - 2x
x+2x = 15 - 3
3x = 12
x = 4
9. Sınıf Matematik Ders Kitabı Sayfa 65-66 Cevapları
1. Yanda verilen Venn şemasına göre aşağıda istenilen kümeleri liste yöntemi ile yazınız.
a) A = ? A = {1, 2, 3, 4, 5}
b) B = ? A = {4, 5, 6, 4}
c) A ∪ B = ? A ∪ B = {1, 2, 3, 4, 5, 6, 7}
ç) A ∩ B = ? A ∩ B = { 4, 5}
d) B \ A = ? B \ A = {6, 7}
2. Yanda verilen Venn şemasına göre aşağıda istenilen kümeleri liste yöntemi ile yazınız.
a) A'= ? A'= {d, e, f}
b) B' = ? B'= {a, b}
c) (A ∩ B)' = ? (A ∩ B)' = {a, b, c, d, e, f}
ç) (A ∪ B)' = ? (A ∪ B)' = { }
d) E' = ? E' = { }
3.
A = {x | x , tek doğal sayılar} = {1, 3, 5 ........}
B = {x | x , çift tam sayılar} = {.........-2, 0, 2, 4, 6 .......}
C = {x | x , pozitif tam sayılar} = {1, 2, 3, 4, 5...............}
kümeleri veriliyor. Buna göre hangi kümelerin ayrık küme belirttiğini bulunuz.
A∩B=∅ boş olduğu için A ve B ayrı kümelerdir.
5. Yandaki şemada sayılar bulundukları bölgeye ait eleman sayılarını belirtmektedir. Buna göre
a) s(A ∪ B) = ? 2+5+3 =10
b) s(A ∩ B) = ? 2
c) s(A \ B) + s(B \ A) değerini bulunuz. 5+3 =8
6.
25 kişilik bir sınıfta
10 kişi matematik dersinden başarılıdır.
16 kişi Türkçe dersinden başarılıdır.
7 kişi her iki dersten de başarısızdır.
Verilenlere göre bir Venn şeması çizerek eleman sayılarını uygun bölgelere yazınız.
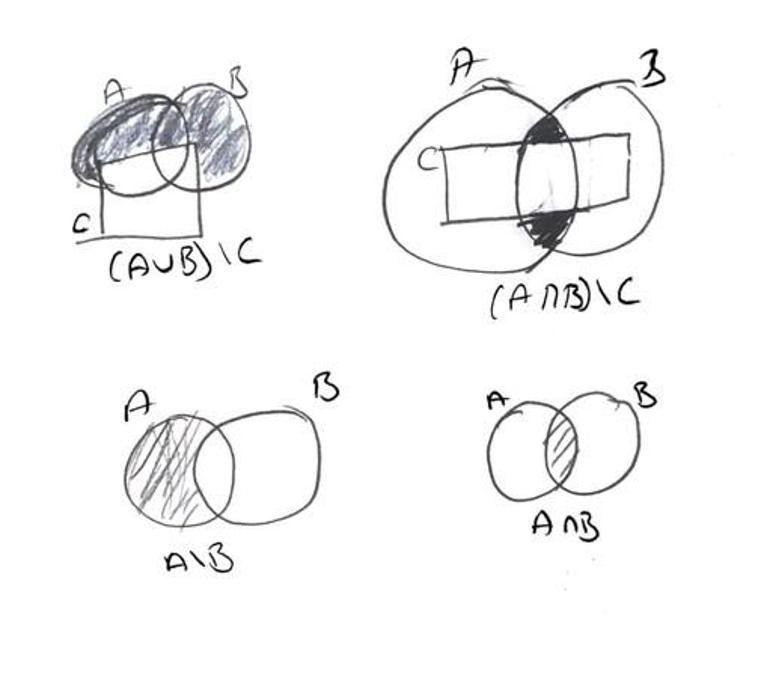
7. Aşağıda verilen Venn şemasına göre istenilenleri bulunuz.
a) H = ? H= {1, 2, 3}
b) E\H' = ? E\H' = {1, 2, 3}
c) E\ (H ∩ M)' = ? E\ (H ∩ M)' = {1, 4, 5, x, y, t=
ç) s(M) + s(M') = ?s(M) + s(M') = 5+3=8
8. A ve B boş kümeden farklı iki küme olmak üzere
Buna göre s(A ∪ B) = 60 ise s(B \ A) nı bulunuz.
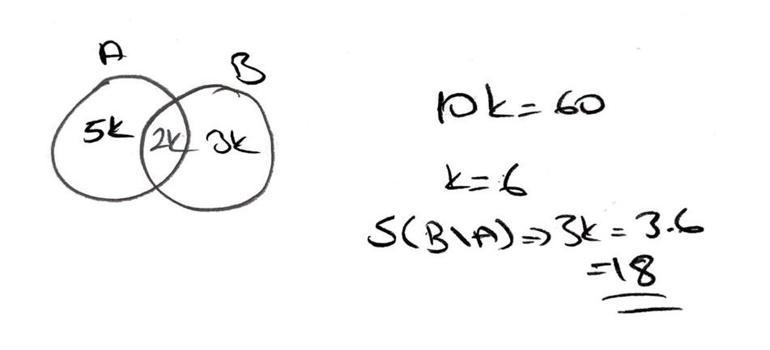
9. A ve B kümeleri E evrensel kümesinin iki alt kümesidir. Buna göre [A ∪ (B ∩ A)'] ∩ [B' ∩ (A ∪ B)] kümesini en sade şekilde yazınız.
[A ∪ (B ∩ A)'] ∩ [B' ∩ (A ∪ B)]
A ∪ A' ∪ B' = E
A ∪ A' ∪ B' ∩ (A \ B)
E ∩ (A \ B) = A \ B
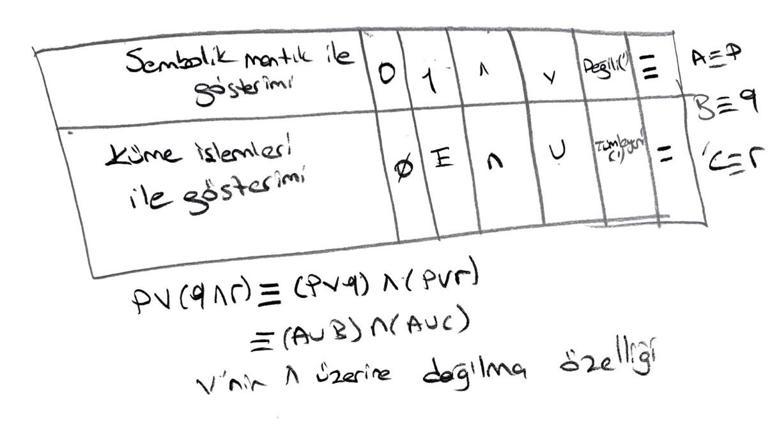
10. A ∪(B∩ C) = (A ∪ B) ∩ (A ∪ C) olduğunu sembolik mantık kurallarını kullanarak gösteriniz.
11. A ∩ A' = ∅ olduğunu sembolik mantık kurallarını kullanarak gösteriniz.
Çözüm:
P Λ P' ≡ ∅
1 Λ 0 ≡ 0
0 Λ 1 ≡ 0
A ≡ P
12. (E \ A)' = A olduğunu sembolik mantık kurallarını kullanarak gösteriniz.
Çözüm:
(E ∩ A')' ≡ (1 Λ P')' ≡ (P')' ≡ P ≡ A
A ≡ P
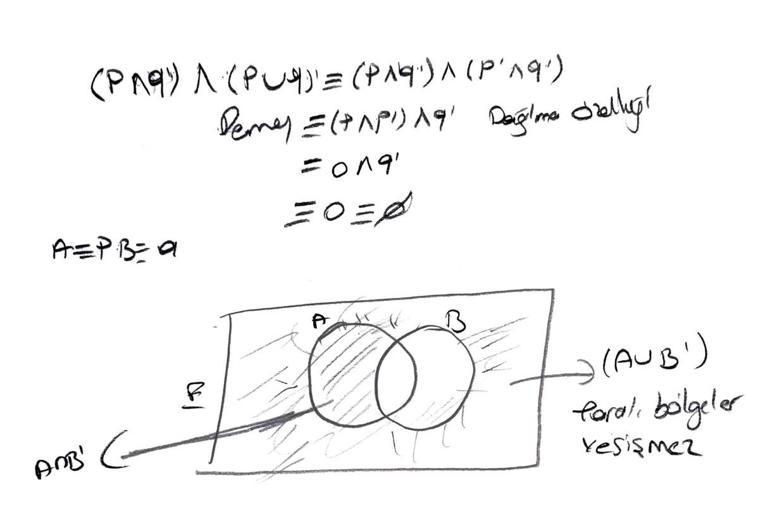
13. (A ∩ B') ∩ (A ∪ B)' küme işlemini sembolik mantık kurallarını kullanarak en sade biçime getiriniz.
9. Sınıf Matematik Ders Kitabı Sayfa 71 Cevapları
1. Bir tatlıcıya giden 20 kişiden 12 si künefe, 9 u baklava, 5 i hem künefe hem baklava yemiştir. Buna göre bu grupta tatlı yemeyen kaç kişi olduğunu bulunuz.
Çözüm:
S(K ∪ B) = 12+9-5= 16
20-16 = 4
2.
34 kişinin çalıştığı bir şirketin dinlenme saatinde,
21 kişi çay içmiştir.
16 kişi kahve içmiştir.
Çay ve kahve içen kişi sayısı, çay veya kahve içmeyenlerin sayısının 2 katıdır.
Buna göre sadece çay içen kaç kişi olduğunu bulunuz.
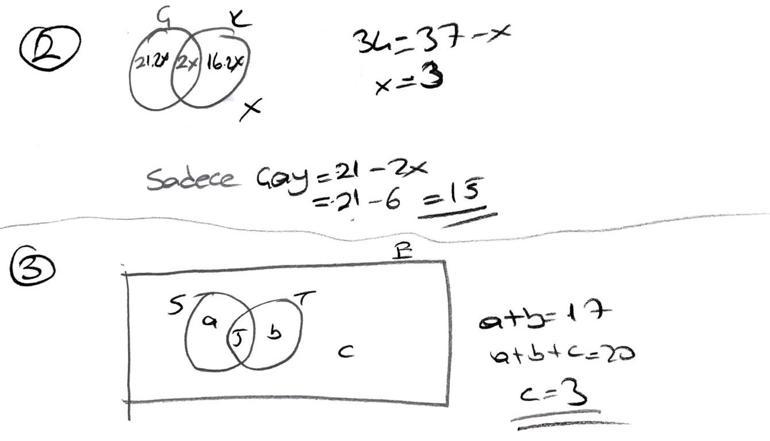
3. Bir fatura ödeme merkezinde sadece elektrik, su ve telefon faturaları ödenmektedir. Bu fatura ödeme merkezine bir saat içinde gelen 25 kişiden hepsi elektrik faturası ödemiştir. Farklı türde iki fatura ödeyen 17 kişi, farklı türde üç fatura ödeyen 5 kişi olduğuna göre sadece elektrik faturası ödeyen kaç kişi olduğunu bulunuz.
4. Bir halk eğitim merkezinde diksiyon, ebru ve el sanatları kursu açılmıştır. Bu kurslardan en az birine katılan 38 kişiden 20 si diksiyon, 18 i ebru ve 19 u el sanatları kursunu tamamlamıştır.
Diksiyon ve ebru kursunu tamamlayan 6 kişi,
Diksiyon ve el sanatları kursunu tamamlayan 9 kişi,
Ebru ve el sanatları kursunu tamamlayan 7 kişi vardır.
Verilenlere göre her üç kursuda tamamlayan kaç kişi olduğunu bulunuz.
Çözüm:
38 = 20 + 18 + 19 - 6 - 9 -7 + x
x = 3
5. Sınıfça yemek yemeye giden bir grup öğrenciden 14 ü et döner 16 sı tavuk döner yemiştir. Soslu döner yiyen 18 kişi olup soslu et döner yiyenlerin sayısı sossuz tavuk döner yiyenlerin 2 katıdır. Her öğrenci birer döner yediğine göre bu sınıfta soslu tavuk döner yiyen kaç öğrenci olduğunu bulunuz.
6. Arapça, Farsça ve Türkçe dillerinden yalnız birini bilenlerden oluşan bir kafilede Arapça bilmeyen 17, Farsça bilmeyen 15 ve Türkçe bilmeyen 10 kişi vardır. Bu kafilede Türkçe bilen kaç kişi olduğunu bulunuz.
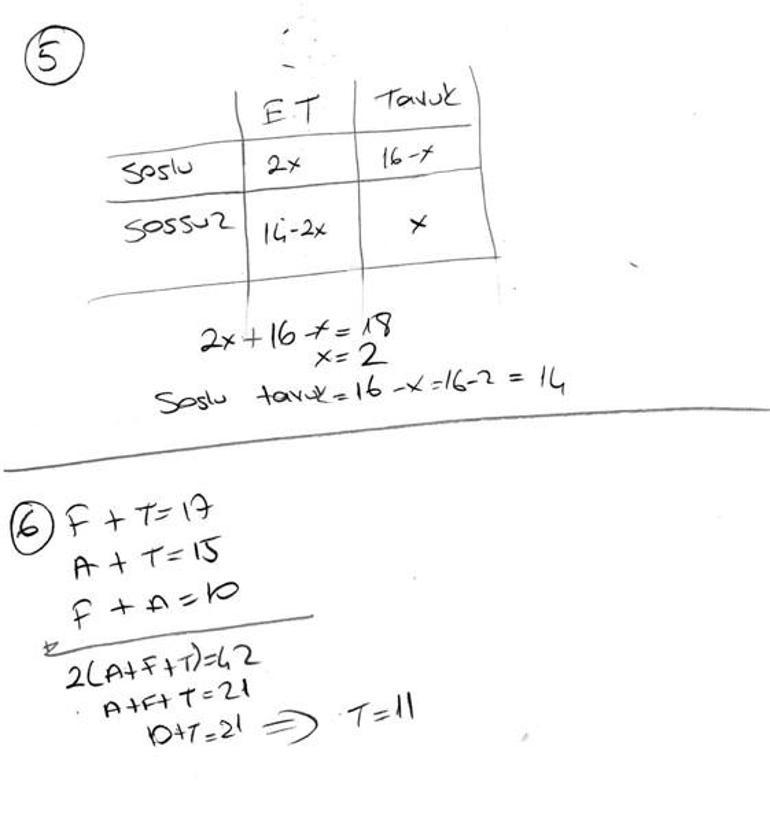
7. 30 kişilik bir sınıfta fizik dersinden başarılı herkes matematik dersinden de başarılı, matematik dersinden başarılı herkes Türkçe dersinden de başarılıdır.
Türkçe dersinden başarısız öğrenci yoktur.
Yanlız iki dersten başarılı öğrenci sayısı üç dersten de başarılı öğrenci sayısının iki katı, yalnız bir dersten başarılı öğrenci sayısından 5 fazladır.
Verilenlere göre en az iki dersten başarılı olan öğrenci sayısını bulunuz.
9. Sınıf Matematik Ders Kitabı Sayfa 76 Cevapları
1. Yandaki grafikte verilen A, B, C, D, E noktaları farklı adaları göstermektedir. Orijinde bulunan geminin kaptanı gemisini A noktasındaki adaya götürecektir. Ancak adaya ulaştığında kaptan adanın koordinatlarının birinci ve ikinci bileşenlerinin yerini karıştırıp farklı bir adaya geldiğinin farkına varmıştır. Buna göre kaptanın gemisini hangi adaya götürdüğünü bulunuz.
Çözüm:
A(10,40)
E(40,10)
2. (x, y) sıralı ikilisinde x ve y birer rakam olmak üzere x + y nin en çok kaç olabileceğini bulunuz.
Çözüm:
9+9=18
3. (2x-2,27) = (64,31–y) eşitliğinde x – y nin değerini bulunuz.
Çözüm:
2x-2 = 64 = 26
x-2 = 6
b = 8
1 - y = 3
y = 2
x-y = 8 - (-2) = 10
4. A = {x | x , rakamlar kümesi} ve B = {x | x , 10 dan küçük ve 2 nin doğal sayı kuvvetleri} dir. Bu durumda s(AxB) değerini bulunuz.
Çözüm:
A = {0,1,2,3,4,5,6,7,8,9} s(A) = 10
B = {1,2,4,8} s(B) = 4
s(AxB)= s(A) x s(B) = 10 x 4 = 40
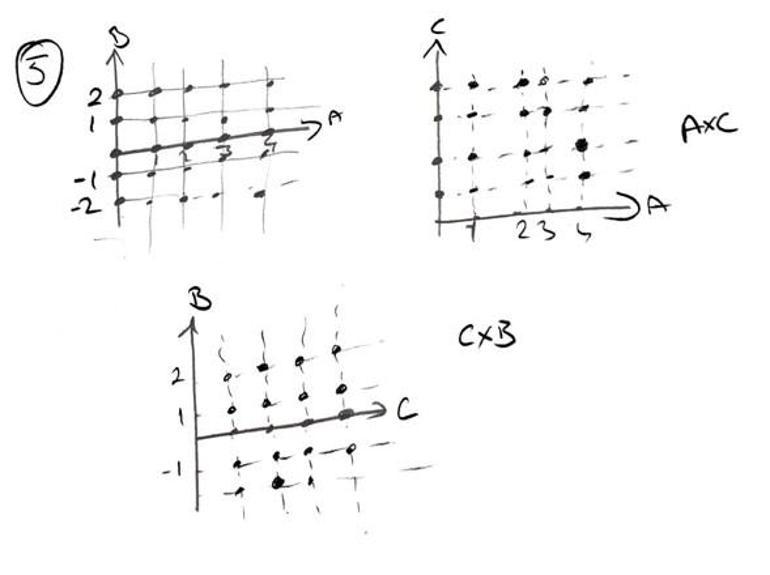
5.
A = {x | -1 < x < 4, x ≡ N }
B = {y | y2 < 9, y ≡ Z } ve
C = {x | x , 6 nın pozitif tam sayı çarpanları} kümeleri veriliyor. AxB, AxC, CxB ifadelerini dik koordinat sisteminde gösteriniz.
6. A = {x | 12 < x < 200, x = 5n, n ∈ Z } ve B = {x | x , alfabemizdeki ünlü harfler} ise s(AxB) değerini bulunuz.
Çözüm:
A = {x | 12 < x < 200, x = 5n, n ≡ Z } = { 15,20,25.....195} : s(A)= (195-15) / 5 + 1 = 37
s(B)= {a,e,u,ü,o,ö,i,ı} = 8
s(AxB)= 37 x 8 = 296
7. (3x + 4y , 2) =(5 , 4x + 3y) eşitliğine göre x + y değerini bulunuz.
Çözüm:
3x + 4y = 5
4x + 3y = 2
7x + 7y = 7
7(x+y) = 7
x+y= 1
9. Sınıf Matematik Ders Kitabı Sayfa 77-78 Cevapları
1.
I. A = {x | x , HAKAN sözcüğündeki harfler} ise s(A) = 4 tür.
B = { ∅ } ise s(B) = 0 dır.
III. C = {y | 1 < y < 7, y iki basamaklı doğal sayı} ise s(C) = 0 dır.
Yukarıda verilenlerden hangisi veya hangileri doğrudur?
A) Yalnız l B) Yalnız lll C) l ve ll D) ll ve lll E) l ve lll
2. A = {x | x ≤ 5, x bir rakam} ise
{2} ∈ A
{1,2} ⊊ A
III. s(A) = 6 dır.
A nın alt küme sayısı 32 dir.
Yukarıda verilenlerden hangisi veya hangileri doğrudur?
A) ll ve lll B) l ve lV C) ll ve lV D) l ve lll E) lll ve lV
3. A = {a | a yı tam bölen farklı pozitif tam sayılar} kümesi veriliyor. s(A) = 4 şartını sağlayan a değeri aşağıdakilerden hangisi olabilir?
A) 9 B) 16 C) 27 D) 36 E) 45
4. A = {a, b, c, d, {1, 2, 3, 4}} alt kümelerinin kaç tanesinde b elemanı bulunup c elemanı bulunmaz?
A) 64 B) 32 C) 16 D) 8 E) 4
5. A = {a, b, c} ve B = {a, b, c, 1, 2, 3} kümeleri veriliyor. B kümesinin alt kümelerinden kaç tanesi A kümesini kapsar?
A) 4 B) 8 C) 16 D) 32 E) 64
6. a ∈ A ve b ∈ A olmak üzere , a ve b elemanlarından yalnız birinin bulunduğu alt küme sayısı 32 ise A nın kendisi hariç alt küme sayısı kaçtır?
A) 15 B) 31 C) 32 D) 63 E) 64
7. A ve B boş kümeden farklı iki küme olsun. A Ç B nin alt küme sayısı 1, A \ B nin alt küme sayısı 8, A U B nin eleman sayısı 9 ise B \ A nın alt küme sayısı kaçtır?
A) 5 B) 8 C) 16 D) 32 E) 64
8. A = {x | x ≤ 40, x = 2n, n ∈ N } kümesi veriliyor.
I. B = {x | x , 41 den küçük çift pozitif tam sayı}
II. C = {x | x , 42 den küçük çift doğal sayı}
III. D = {x | x, 40 tan küçük pozitif tam sayı}
Yukarıda verilenlerden hangisi ya da hangileri A kümesine eşittir?
A) Yalnız l B) Yalnız ll C) l ve ll D) ll ve lll E) l-ll-lll
9. Yukarıdaki Venn şemasına göre s (A ∩ B') + s(B') toplamı kaçtır?
A) 6 B) 7 C) 8 D) 9 E) 10
10. A ⊊ E, A ¹ ∅ ve A ¹ E olmak üzere
I. A ∩ A'
II. A U A'
III. A Ç E
IV. A' ∩ E
ifadelerinden hangisi ya da hangileri boş küme belirtir?
A) Yalnız l B) l ve lV C) ll ve lll D) lll ve lV E) l ve ll
11. A = {x | x, 3 veya 4 ün katı olan iki basamaklı doğal sayı} B = {x | x, 12 ile bölünebilen iki basamaklı doğal sayı} ise s(A) – s(B) kaçtır?
A) 52 B) 48 C) 44 D) 36 E) 35
12.
A = {x | 13 < x < 70, x = 3k, k ∈ N }
B = {y l 2 ≤ y < 50, y = 5k, k ∈ N } ise s(A U B) kaçtır?
A) 39 B) 35 C) 32 D) 28 E) 25
13. Boş kümeden farklı A ve B kümeleri için s(A , B) = 2. s(A + B) = 3.s(A = B) ise ( ) ( ) s B s B = A değeri kaçtır?
A) 5/2
B) 4/3
C) 4/1
D) 5/1
E) 5/2
14. A ve B kümeleri için s(A \ B’) = 5 , s(A) = 8 ve s(A , B) =17 ise s(B) nın değeri kaçtır?
A) 13 B) 14 C) 15 D) 16 E) 17
15. 24 kişilik bir sınıfta kimya veya fizik derslerinden geçenler ile kalanlar vardır. Kimya veya fizik derslerinden kalanların sayısı 4, yalnız bir dersten geçen 12 kişi ise her iki dersten geçen kaç kişi vardır?
A) 8 B) 10 C) 11 D) 12 E) 14
16.
40 kişilik bir spor kulübünde,
Yalnız basketbol oynayanların sayısı, futbol oynayanların sayısına eşittir.
Yalnız futbol oynayanların sayısı, futbol veya basketbol oynamayanların sayısına eşittir.
Futbol veya basketbol oynamayanların sayısı, her iki oyunu oynayanların 2 katına eşittir.
Bu kulüpte futbol ya da basketbol oynayan kaç kişi vardır?
A) 35 B) 30 C) 28 D) 25 E) 20
17.Yukarıdaki Venn şemasında verilen taralı bölgeleri ifade eden küme aşağıdakilerden hangisidir?
A) (A , C) \ (B , C)
B) (A , B)’ \ C
C) (A , B) \ C
D) (A + B) \ C
E) (A + B)’ \ (B + C)’
18. A = {1, 2} ve B = {1, 2, 3, 4, 5, 6, 7} kümeleri veriliyor. A 3 K 3 B ise K ≠ A olmak üzere kaç farklı K kümesi vardır?
A) 7 B) 15 C) 16 D) 31 E) 32
19. A, B 3 E olmak üzere 6E = (A = Bl) + (Al + Bl) ifadesinin en sade biçimi aşağıdakilerden hangisidir?
A) A \ B B) B \ A C) E D) A E) B
20. Yukarıdaki Venn şemasında verilen taralı bölgeler aşağıdakilerden hangisi ile ifade edilebilir?
A) (A \ B) , (B , C)
B) (A + B + C ) , (A \ B)
C) A , (A + B)
D) (B + C) , A
E) (A\(B , C)) , (A + B + C )
21. A = {1, 2, 3, 4} kümesi veriliyor. (A \ B) , (B \ A) = {0, 2, 4, 6, 8} olduğuna göre B kümesinin eleman sayısı kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
22. A = {-1, 0, 1, 2}, B = {1, 2, 3} ve C = {2, 3, 4} tür. AxB ve BxC kümelerinin kaç tane ortak elemanı vardır?
A) 1 B) 2 C) 3 D) 4 E) 5
23. A = {(x, y) | y=3x + 1, x ve y rakam} kümesinin eleman sayısı kaçtır?
A) 3 B) 4 C) 5 D) 6 E) 7
24. A = {-1, 0, 2, 3} ve B = {2, 3, 5} kümeleri veriliyor. AxB grafiğindeki noktalardan herhangi dördünü köşe kabul ederek çizilebilen en büyük alanlı dikdörtgenin çevresi kaç birimdir?
A) 8 B) 9 C) 10 D) 12 E) 14
25. A ve B, E evrensel kümesinin iki alt kümesi olmak üzere 3 . s(A \ B) = 6 . s(A + B) =2 . s(B + Al ) ve s(A , B) = 42 ise s(A) nın değeri kaçtır?
A) 7 B) 14 C) 21 D) 23 E) 25
9. Sınıf Matematik Ders Kitabı Sayfa 87 Cevapları
1. 6/5 sayısının N,Z,Z+,Z-,Q,Q',Q+,Q-,R,R+,R-sembolleri ile gösterilen sayı kümelerinin hangilerinin elemanı olduğunu bulunuz.
Cevap: Q, Q+ , R, R+
2. x ve y birer tam sayı olmak üzere
(D) a) x2 + y3
(Y) b) x/y
(D) c) -4 . x3 . y5
(Y) ç) √ x . y - 6
(D) d) xy
ifadelerinden hangilerinin daima bir rasyonel sayı belirttiğini bulunuz.
3. 3. m ve n birer pozitif tam sayı olmak üzere 2m + 3n = 25 eşitliğini sağlayan n sayısının alabileceği en büyük ve en küçük değerlerin toplamını bulunuz.
En büyük m = 2 için
2m + 3n = 25 : 2 . 2 + 3n = 25 : 3n = 25 - 4
n = 21 / 3 = 7
En küçük m = 11 için
2m + 3n = 25 : 2 . 11 + 3n = 25 : 3n = 25 - 22
n = 3 / 3 = 1
4. a,b,c birer negatif tam sayı olmak üzere
a.b=24
b.c = 30 ise a + b + c toplamının alabileceği en büyük ve en küçük değerleri bulunuz.
En küçük
a = -24
b = -1
c = -30
a + b + c = -24 + (-1) + (-30) = -55
En büyük
a = -4
b = -6
c = -5
a + b + c = -4 + (-6) + (-5) = -15
5. a, b ve c birer doğal sayı olmak üzere a + b + c = 18 ise a . b . c ifadesinin alabileceği en büyük ve en küçük değerleri bulunuz.
En küçük
a = 0
b = 0
c = 18
a . b . c = 0 . 0 . 18 = 0
En büyük
a = 6
b = 6
c = 6
a . b . c = 6 . 6 . 6 = 216
6. a, b ve c birer tam sayı olmak üzere a . b . c = 75 ise a + b + c ifadesinin alabileceği en büyük ve en küçük değerleri bulunuz.
En küçük
a = -75
b = -1
c = 1
a + b + c = -75 + (-1) + 1 = -75
En büyük
a = 75
b = 1
c = 1
a + b + c = 75 + 1 + 1 = 77
7. x ve y sayıları birer gerçek sayı olmak üzere x + y = 7 ise x ∙ y ifadesinin alabileceği en büyük değeri bulunuz.
x = 7/2
y = 7/2
x . y = 7/2 . 7/2
x . y = 49 / 4
8. a, b, c birbirinden farklı pozitif tam sayılar olmak üzere a + 2b + 3c ifadesinin alabileceği en küçük değeri bulunuz.
a = 3
b = 2
c = 1
a + 2b + 3c = 3 + 2.2 + 3.1 = 3 + 4 + 3 = 10
9. a ve b tam sayılar olmak üzere a . b = 6 denklemini sağlayan kaç tane (a , b) sıralı ikilisi olduğunu bulunuz.
(a,b) = (1,6), (6,1), (3,2), (2,3), (-1,-6), (-6,-1), (-3,-2), (-2,-3)
Toplam 8
10. a ve b birer tam sayı olmak üzere (a + 3) √2 + (b – 5) √ 7 ifadesinin bir rasyonel sayı belirtebilmesi için a ∙ b değerini bulunuz.
a + 3 = 0 -: a = -3
b - 5 = 0 -: b = 5
a . b = -3 . 5 = -15
9. Sınıf Matematik Ders Kitabı Sayfa 96-97 Cevapları
1. Yandaki bölme işleminde x doğal sayısının alabileceği en büyük değer için A doğal sayısının değerini bulunuz.
Çözüm:
x<13
x=12 En küçük
A=13.7+x=91+12=103
2. Yukarıdaki bölme işlemlerine göre A nın C türünden yazılışını bulunuz.
3. Altı basamaklı 981 984 sayısının 981 ile bölümünden elde edilen bölüm ile kalanın toplamını bulunuz.
4. Aşağıdaki sayı ikililerinden hangisi aralarında asal değildir?
A) (12,95) B) (11,145) C) (1,24) D) (3,112) E) (13,1001)
5. Dört basamaklı 6m35 sayısının 3 ile bölümünden kalan 1 ise m nin alabileceği değerler toplamını bulunuz.
6+3+5+m=3.k+1
14+m=3k+1
13+m=3k=15,18,21
m=2,5,8
2+5+8=15
6. Rakamları farklı beş basamaklı 378A2 doğal sayısı 4 ün bir tam katı olduğuna göre A'nın alabileceği değerler toplamını bulunuz.
Verilen sayının 4’ün tam katı olabilmesi için son iki rakamının 4’e tam olarak bölünebilmesi gerekir.
Bu durumda A’nın alabileceği değerler: 1 / 3 / 5 / 7 / 9 olacaktır.
7. Bir fabrikanın işletme bölümünde çalışan Ayla Hanım, satılan ürün sayısı ve toplam satış fiyatlarını bilgisayara girerken faturada, birim satış fiyatı ₺11 olan bir ürünün toplam ₺174342 şeklinde olduğunu ve tutarın onlar basamağındaki sayısının silindiğini görmüştür. Buna göre bu fabrikanın bu üründen toplam kaç adet sattığını bulunuz.
8. Beş basamaklı 41A7B doğal sayısının 36 ile bölümünden kalan 15 olduğuna göre A sayısının kaç farklı değer alabileceğini bulunuz.
9. X doğal sayısının 13 ile bölümünden kalan 11 ve Y doğal sayısının 13 ile bölümünden kalan 7 ise
a) X + Y nin 13 ile bölümünden kalanı bulunuz.
b) X ∙ Y nin 13 ile bölümünden kalanı bulunuz.
10. Dört basamaklı 6m2n sayısının 4 e bölümünden kalan 2 ve 9 a bölümünden kalan 1 ise m + n toplamının kaç farklı değer alabileceğini bulunuz.
11. M doğal sayısının 6 ile bölümünden kalan 4 olduğuna göre aşağıdaki ifadelerin 6 ile bölümünden kalanı bulunuz.
a) 3M + 3
b) 2M - 4
c) 4M + 2
ç) M + 6
9. Sınıf Matematik Ders Kitabı Sayfa 104-105 Cevapları
1. 8'e , 12'ye ve 20'ye bölünebilen 600 den küçük, en büyük pozitif tam sayısını bulunuz.
8 e , 12 ye ve 20 ye bölünebilen sayıyı bulabilmek için bu sayıların en küçük ortak katını (ekok) bulmamız gerekir.
Gösterilen şekilde ekok 120 olarak bulunur.
600 den küçük denildiği için 120 nin 600 den küçük katlarına bakmalıyız.
120, 240, 360,480 ve 600 diye devam ederken 600 den küçük olarak en büyük 480 sayısı bulunur.
Cevap 480 dir.
8 12 20 | 2
4 6 10 | 2
2 3 5 | 2
1 3 5 | 3
1 5 | 5
1
120 x 4 = 480
2. 156 ve 442 sayılarını tam bölen en büyük doğal sayının rakamları toplamını bulunuz.
Ortak bölenler iki türlüdür. Ebob ve Ekok olmak üzere iki gruba ayrılır.Ebob demek ''b '' harfi ile en büyük böleni çağrıştırmaktadır.Ekok ise '' k '' harfi ile en küçük böleni çağrıştırmaktadır.
Ortak bölenlerini EBOB ile bulabiliriz.Ebob,her ikisininde ortak böleni olmasıdır.
442 156 / 2*
221 78 / 2
221 39 / 3
221 13/ 13*
17 1 /17
1
(156, 442) ebob = 2 . 13 = 26 Ebob '' 26 '' sayımızın rakamlarının toplamı : 2+6 =8 olur.
3. Bir çiçekçi güllerini üçerli, beşerli ve sekizerli saydığında her defasında 2 gül artmaktadır. Gül sayısı 200 den fazla olduğuna göre bu çiçekçinin en az kaç gülünün olduğunu bulunuz.
Soruyu çözebilmemiz için öncelikle 3, 5 ve 8 in en küçük ortak katını bulmamız gerekiyor. O halde:
3x5x8=120 (sayılar aralarında asal olduğu için direkt çarptık)
120 sayısı 3, 5 ve 8 ile tam bölünen en küçük sayıdır. Soruda 3, 5 ve 8 ile bölümünden kalanın 2 olması gerektiği verilmiş. O halde bu sayıya 2 ekleyelim:
120+2=122 ==> Güllerin 200'den fazla olması gerekiyor. 122 sayısına 120 eklersek hem güller 200 den fazla olur hem de 3, 5 ve 8 ile bölümünden 2 kalma şartı korunmuş olur. O halde:
122+120=242
Çiçekçinin en az 242 gülü vardır.
4. a, b, c sayıları birer doğal sayıdır. K = 3a + 1 = 4b + 2 = 5c + 3 olduğuna göre K nin en küçük değerini bulunuz.
5. Boyları 120 cm, 135 cm ve 180 cm olan üç demir çubuk eşit büyüklükte ve artmayacak şekilde parçalara ayrılacaktır. Bu iş için en az kaç kesim yapılması gerektiğini bulunuz (Çubuklar ayrı ayrı kesilecektir).
büyük parçalardan küçük parçalara bölünme işlemi olduğu için ebob sorusudur (120,135,180 )ebob=
120 135 180 | 2
60 135 90 | 2
30 135 45 | 2
15 135 45| 3 +
5 45 15 | 3
5 15 5 | 3
5 5 5 | 5 +
1 1 1 ise EBOB(120,135,180)=15 deriz
çubuklar ayrı ayrı kesilecek ise hepsine ayrı işlem yapılmalıdır.
ÇUBUK (120)
120/15 = 8 8 PARÇAYI KESMEK İÇİN 7 KESİM YAPILIR
ÇUBUK (135)
135/15 = 9 9 PARÇAYI KESMEK İÇİN 8 KESİM YAPILIR
ÇUBUK (180)
180/15 = 12 12 PARÇAYI KESMEK İÇİN 11 KESİM YAPILIR
7+8+11= 26 kesim yapılır.
6. Boyutları 4 cm, 5 cm ve 6 cm olan dikdörtgenler prizmasından en az kaç tanesi yan yana ve üst üste getirilirse bir küp oluşur? Bulunuz.
Öncelikle küp oluşturmak için bütün kenarların eşit olması gerekiyor. En az dikdörtgen prizma kullanarak dediği için:
4, 5 ve 6 nın en küçük ortak katını bulmamız gerekiyor:
4 5 ve 6 'nın en küçük ortak katı 60'tır. O halde:
60/4=15
60/5=12
60/6=10
10+12+15=37 tane kullanarak bir küp oluşturabiliriz.
7. A, B, C firmaları Yozgat İstanbul arasında sırasıyla 3 günde, 4 günde ve 5 günde bir sefer düzenliyor. Bu firmalar birlikte ilk seferlerine başladıktan kaç gün sonra 2. kez birlikte tekrar sefere çıkacaklarını bulunuz.
EKOK(3,4,5) = 60
1. kez 60 gün sonra
2. kez 120 gün sonra birlikte sefere çıkarlar
9. Sınıf Matematik Ders Kitabı Sayfa 108 Cevapları
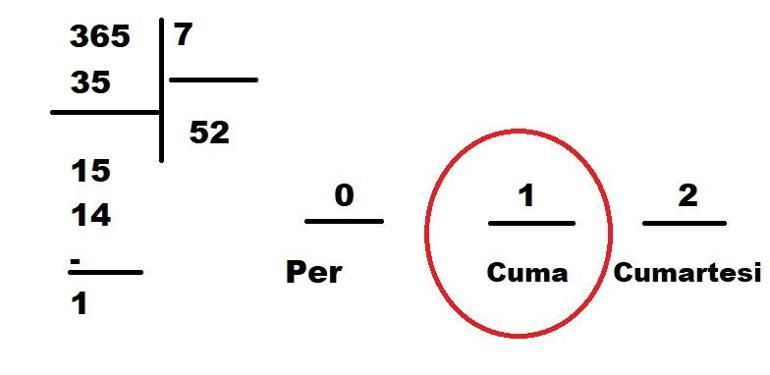
1. 14 Aralık 2017 Perşembe günü olduğuna göre 14 Aralık 2018 tarihinin hangi gün olacağını bulunuz (2017 ve 2018 yılı 365 gündür.).
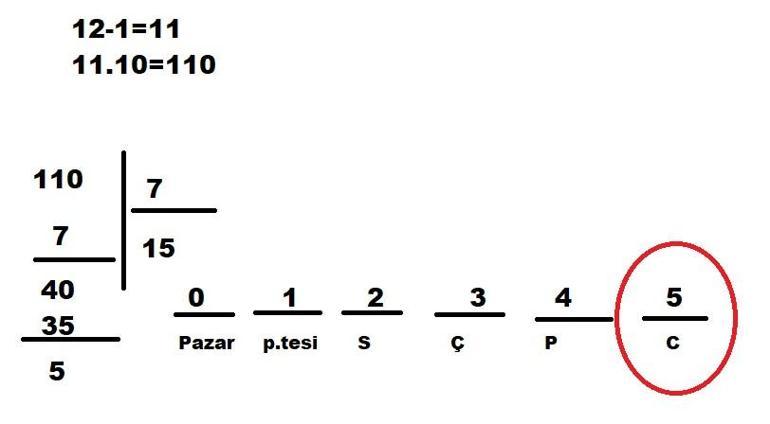
2. Üniversite sınavına hazırlanan İbrahim 10 günde bir deneme sınavı çözmektedir. İlk denemesini pazar günü çözen İbrahim, 12. denemesini hangi gün çözeceğini bulunuz.
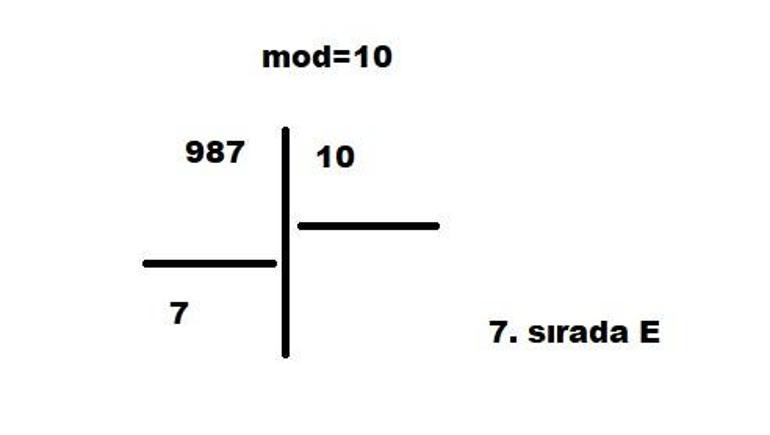
3. Yukarıdaki şekilde bulunan 6 lamba , A – B – C – D – E – F – E – D – C – B – A – B – … sırasıyla yanıp sönmektedir. Buna göre bu döngüde 987. sırada yanacak olan lambanın hangi harfle gösterildiğini bulunuz.
4.
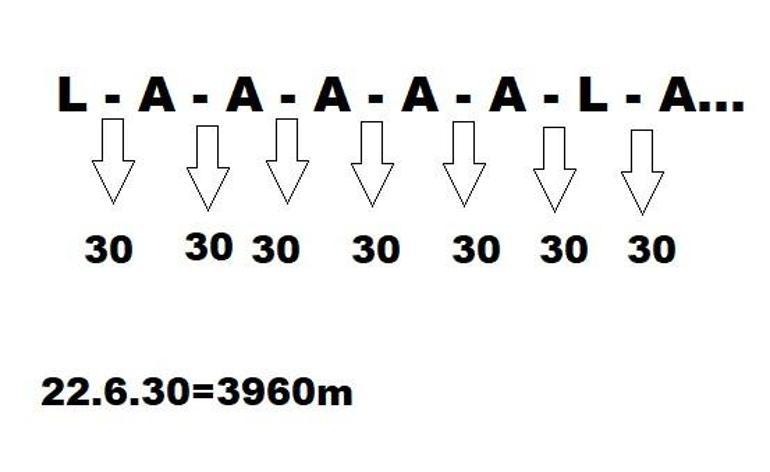
Bir belediye doğrusal bir yol boyunca orta refüj çalışmasını aşağıdaki gibi yapmıştır.
Yol boyunca otuzar metre aralıklarla çukurlar açılmıştır.
Her çukura ağaç ya da aydınlatma lambası dikilmiştir.
Her 5 ağaç arasına bir aydınlatma lambası dikilmiştir.
Evlerinin önünde aydınlatma lambası olan Gülnaz evden çıkıp bu yol boyunca ilerleyerek okuluna gitmiş ve okulun önünde de aydınlatma lambası görerek okuluna ulaşmıştır. Yol boyunca 23 tane aydınlatma lambası gördüğüne göre Gülnaz’ın evinin okuluna uzaklığının kaç metre olduğunu bulunuz.
9. Sınıf Matematik Ders Kitabı Sayfa 111 Cevapları
1. Aşağıda verilen kümeleri aralık biçiminde yazıp sayı doğrusu üzerinde gösteriniz.
a) A={x | -4 < x ≤ 8, x ∈ R }
b) B={x | x < 7, x ∈ R }
c) C={x | -8 < x < 0 , x ∈ R }
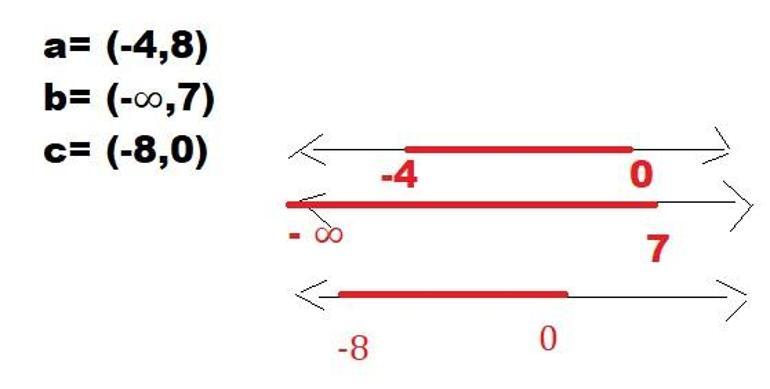
2. Aşağıda sayı doğrusu üzerinde kırmızı renk ile gösterilen kümeleri aralık biçiminde yanlarındaki boşluklara yazınız.
a= [-4,2)
b= (-2, ∞)
c= (-3, 3)
3. A = [-7,0) ve B = (-2, ∞) olmak üzere aşağıdaki istenilenleri aralık belirtecek şekilde cevaplandırınız.
a) A ∩ B = (-2,0)
b) A ∩ B = [-7, ∞)
c) (A \ B)' = A\B= [-7,-2] → (A\B)′= R-[-7,-2]
ç) (AUB)' = (-∞, -7)
4. A={x | x < 5, x ∈ R } olarak veriliyor. Buna göre aşağıdaki istenilenleri aralık belirtecek şekilde cevaplandırınız.
a) R U A
R= (-∞,∞)
b) R ∩ A
(-∞,5)
c) (R \ A)
[5,∞)
ç) (R \ A)′
(-∞,5)
9. Sınıf Matematik Ders Kitabı Sayfa 120 Cevapları
1. -6 ∙ (2x + 4) + 4x = 8x + 40 denkleminin çözüm kümesini bulunuz.
Çözüm:
-12x - 24 + 4x = 8x + 40
-8x -8x = 40 + 24
-16x = 64
x = -4
2. 3x – 5 – [x + 6 – 2(9 + 3x)] = 0 denkleminin çözüm kümesini bulunuz.
Çözüm:
3x – 5 – [x + 6 – 2(9 + 3x)] = 0
3x - 5 - x - 6 + 18 + 6x = 0
8x + 7 = 0
8x = -7
x = -7/8
3. [(2x + a -5) / (ax - 7)] = x +1 / x - 1 denkleminin kökü 4 olduğuna göre a değerini bulunuz.
Çözüm :
x'in yerine 4'ü yazalım
[(2x + a -5) / (ax - 7)] = x +1 / x - 1
(2.4 + a - 5 / a. 4 - 7) = 4 + 1 / 4 - 1
(8 + a - 5 / 4a - 7) = 5 / 3
(3 + a / 4a - 7) = 5 / 3
İçler dışlar çarpımı yapalım
20a - 35 = 9 + 3a
20a - 3a = 9 + 35
17a = 44
a = 44 / 17
4. m, n d R olmak üzere -m ∙ (2x – 6) + 6x – n = 0 denkleminin çözüm kümesinin tüm gerçek sayılar olabilmesi için m ve n değerlerini bulunuz.
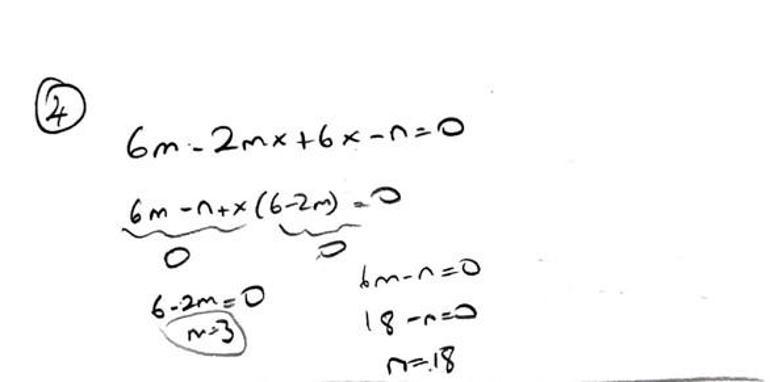
5. x E R olmak üzere -2 ≤ x - 4 / 3 < 4 ise x in değer aralığını bulup sayı doğrusu üzerinde gösteriniz.
Çözüm :
-6 ≤ x - 4 < 12
-2 ≤ x < 16
<-------------- -2............................16 --------:
6. a d R olmak üzere -4 < a ≤ 5 eşitsizliği veriliyor. -3a + 7 ifadesinin alabileceği kaç farklı tam sayı değerinin olduğunu bulunuz.
Çözüm :
- 15 ≤ -3a < 12
-8 ≤ 3a + 7 < 19
19 - (-8) = 27 tane
7. x, y E R olmak üzere
5 < x – 2 ≤ 9 : 7 < x ≤ 11
-3 ≤ y + 3 ≤ 6 : -6 ≤ y ≤ 3 : -3 ≤ -y ≤ 6
8. 3x – 6 ≤ 4x + 2 < 2x + 10 eşitsizliğini sağlayan x gerçek sayılarının alabileceği kaç farklı tam sayı değeri olduğunu bulunuz.
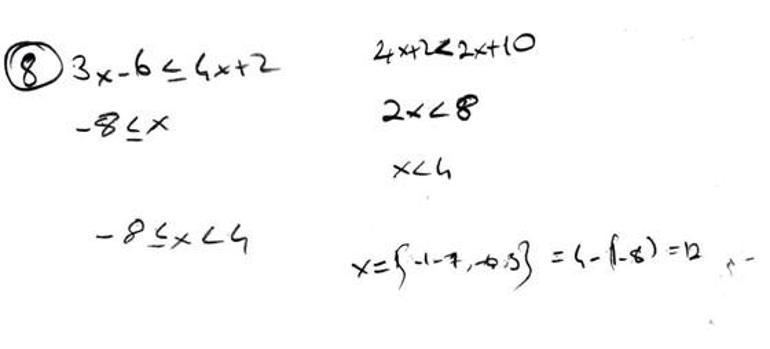
9. Sınıf Matematik Ders Kitabı Sayfa 128 Cevapları
1. Aşağıda verilen ifadeleri mutlak değer dışına çıkarınız.
a) x ∈ R ve x > 0 ise |5x + 7|
b) x ∈ R ve x < 0 ise |3a - |- a||
c) a, b ∈ R ve 0 < a < b ise |a - b| - |b - a|
ç) x, y ∈ R ve x < y < 0 ise |x + y| + |- x| - |y|
a) x ∈ R ve x > 0 ise |5x + 7| dışarı 5x+7 olarak çıkar çünkü x zaten pozitif bir sayıdır dolayısıyla 5x+7 de pozitiftir dışarı aynı şekilde çıkar.
b) x ∈ R ve x < 0 ise |3x - |- x||
I-xI dışarıya -x olarak çıkar çünkü x negatif bir sayıdır önüne - işareti gelince pozitif olur. I3x-(-x) I=I4xI oldu, I4xI dışarıya pozitif olması için -4x olarak çıkar
c) a, b ∈ R ve 0 < a < b ise |a - b| - |b - a|
(a-b) negatif bir sayıdır çünkü b a dan büyüktür.Bu yüzden Ia-bI dışarıya önüne - alarak b-a olarak çıkar.
(b-a) pozitif bir sayıdır çünkü b a dan büyüktür.Bu yüzden Ib-aI dışarıya pozitif olduğu için aynı şekilde çıkar b-a olur.
(b-a)-(b-a)=0 olur.
d) x, y ∈ R ve x < y < 0 ise |x + y| + |- x| - |y|
Ix+yI ifadesi x ve y negatif olduğu için negatif bir sayıdır ve mutlak değer dışına önüne - alarak çıkar -x-y olur
x negatif bir sayı olduğu için -x pozitif bir sayıdır bu yüzden I-xI ifadesi dışarıya aynı şekilde -x olarak çıkar
y negatif bir sayıdır bu yüzden IyI dışarıya önüne - alarak çıkar -y olur
-x-y-x-(-y)=-2x oldu
2. Aşağıda verilen mutlak değerli denklemlerin çözüm kümelerini bulunuz.
a) x ∈ R , |- 2x + 7| = 11
b) x ∈ R , |- 7x + 17| = -2
c) a ∈ R , |5a - 20| = 0
ç) b ∈ R , |- 3b| + |2b| - 20 = 0
a) Mutlak değerin içini önce 11'e daha sonra da -11'e eşitleyerek işlem yapacağız. Mutlak değer bütün sayıları pozitif yaptığından dolayı içindeki sayıların negatif olma ihtimalini de düşünmüş oluyoruz böylece.
-2x + 7 = 11
-2x = 4
x = -2
-2x + 7 = -11
-2x = -18
x =9
Bu işlemlerden anlarız ki x'in -2 ve 9 olmak üzere iki değeri olabilir.
b) Mutlak değerin eşit olduğu sayı hiçbir zaman negatif olamayacağı için x yerine hangi sayıyı yazarsak yazalım bu ifade sağlanamaz. Yani x değerini sağlayan elemanlar kümesi aslında bir boş kümedir.
c) Mutlak değerin içindeki sayı 0 ise eşit olduğu sayı da 0 olur. O halde;
5a - 20 = 0
5a = 20
a = 4 olmalıdır.
ç) Bu soruyu çözerken iki ihtimal için işlem yapmalıyız. b sayısı negatif veya pozitif olabilir. Her ikisini de değerlendirmeliyiz.
* b < 0
-3b -2b = 20
-5b = 20
b = -4
* b > 0
3b + 2b = 20
5b = 20
b = 4
Yani b sayısı -4 veya +4 olabilir.
3. Aşağıda verilen mutlak değerli eşitsizliklerin çözüm kümelerini bulunuz.
a) x ∈ R , |5x - 5|< 10
b) a ∈ R , |7a - 13| < 0
c) a ∈ R , |6a - 12| < -7
ç) a ∈ R , |2a - 2| - 8 ≤ 0
d) x ∈ R , |x + 6| > 0
e) x ∈ R , 6 ≤ |x - 8| ≤ 10
a) |5x - 5| = 10
Mutlak değerin içinin negatif veya pozitif olmasına göre işlemi iki kere yapacağız.
* -5x + 5 =10
-5x = 15
x = -3
* 5x - 5 =10
5x = 15
x = 3
Bu sayılar mutlak değerin içini 0 yapan sayılardır. Yerine yazdığımızda 10'dan küçük gelmesi gerektiği için x çözüm kümesi (-3 , +3) olarak bulunur.
b) Bu ifade mutlak değerin sonucunun 0'dan küçük olmasını istiyor bizden. Ancak mutlak değer sonucu her zaman pozitif olduğu için bu ifade yanlıştır. x yerine yazılabilecek bir sayı yoktur. x kökleri boş kümeyi ifade eder diyebiliriz.
c) | x + 6| > 0
Mutlak değerin sonucu her zaman pozitiftir. Mutlak değer içini 0 yapan değer hariç tüm sayılar x değeri olabilir. Yani x "-6" hariç tüm sayılardır.
ç) Bu seçeneği değerlendirirken mutlak değer içindeki sayının negatif olması ihtimalini de düşüneceğiz. Şöyle düşünebiliriz; (x-8) sayısı mutlak değer içinde olduğu için dışarıya daima pozitif çıkacaktır. x yerine yazdığımız değer sonucu bu sayı 6 da olabilir -6 da olabilir ancak sonuç her zaman 6 olmalıdır.
* 6 ≤ x-8 ≤ 10
14 ≤ x ≤ 18
Bu işlemlerden x sayısı 14, 15, 16, 17 ve 18 çıkar.
* -6 ≥ x-8 ≥ -10
2 ≥ x ≥ -2
Bu işlemlerden de x sayısı 2, 1 , 0, -1 ve -2 olarak bulunur.
x yerine 10 tane sayı yazılabilir ve bu sayılar {-2,-1,0,1,2,14,15,16,17,18}'dir.
4. x ∈ R olmak üzere ||x - 4| - 6| = 2 denkleminin çözüm kümesini bulunuz.

5. x, y ∈ R olmak üzere |x - 3| < 5 ve 3x - y = 2 ise y nin alabileceği kaç farklı tam sayı değeri olduğunu bulunuz.
6. Sayı doğrusu üzerinde 7 ye olan uzaklığı 5 birimden fazla olmayan kaç tane tam sayı değerinin olduğunu bulunuz.
Bir sayı doğrusu üzerine tam sayıları yazdığımızı düşünelim. 7 noktasına olan uzaklığı 5 birimden fazla olmayan tam sayıları yani en fazla 5 birim olan sayıları tek tek işaretleyelim.
7-5 = 2
Sayı doğrusunda 7'ye 5 birim uzaklığındaki en küçük sayı 2'dir.
7+5 = 12
Sayı doğrusunda 7'ye 5 birim uzaklığındaki en büyük sayı 12'dir.
Soruda bizden istenen sayılar 2 ile 12 arasında kalan sayılardır. 2 ve 12 de bu sayılara dahildir.
2, 3, 4, 5, 6, 8, 9, 10, 11, 12
Toplam 10 tane sayı vardır.
7. 2/|a - 2| > 1/3 eşitsizliğini sağlayan kaç farklı a tam sayısının olduğunu bulunuz (a nın 2 olamayacağına dikkat ediniz.).
Öncelikle her iki sayının da pay kısmını eşitleriz. Böylece paydalar arasında kıyaslama yapabiliriz.
Paydaya 2 değerini de yazamayacağımız için özellikle dikkat etmeliyiz. İşlemleri ekte bulabilirsin.
2 / (1a - 21) > 1 / 3
2 / (1a - 21) > 2 / 6
6 > 1a - 21
6 > a - 2 > -21
a = {7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3}
9. Sınıf Matematik Ders Kitabı Sayfa 137 Cevapları
1. A = {(0,4), (1/2,3), (-1,5), (5,2/3), (3,2)} kümesinin elemanlarından kaç tanesinin 2x + 3y = 12 denklemini sağladığını bulunuz.
Parantez içinde verilen değerlerden ilki x, ikincisi y değeridir. Şimdi tek tek değerleri verip denklemde yerine koyup deneyelim ;
(0,4) için x=0,y=4 2.0+3.4=12 (sağladı)
(1/2,3) için x=1/2,y=3 2.1/2+3.3=10 (sağlamadı)
(-1,5) için x=-1,y=5 2.-1+3.5=13 (sağlamadı)
(5,2/3) için x=5,y=2/3 2.5+3.2/3=12 (sağladı)
(3,2) için x=3,y=2 2.3+3.2=12 (sağladı)
3 ifade denklemi sağlar.
2. Aşağıda verilen denklem sistemlerinin çözüm kümelerini bulunuz.
a) -5x + 3y = 22
2x - 3y = -16
b) 7a - 3b = 10
2a + 5b = -3
c) x/2 + y/3 = -1
2x/3 - y/2 = 10
ç) 1/(x+1) - 2y = -11
x/(x+1) + 4y = 22
a) y değerini yok edelim. Böylece x değerinin bulabiliriz.
-5x + 3y = 22
2x - 3y = -16
Bu iki denklemi alt alta toplarsak y değeri yok olacaktır.
-3x = 22-16 = 6
x = -2 olur.
x yerine -2 sayısını yazdığımızda y değerini buluruz.
10 + 3y = 22
3y = 12
y = 4 olur.
b) İki denklemi genişletmemiz gerekecek bu soruda. İlk denklemi 5 ile ikinci denklemi de 3 ile genişletirsek bilinmeyen bir değeri yok etmiş oluruz.
35a - 15b = 50
6a + 15b = -9
İki denklemi toplarız.
41a = 41
a = 1 buluruz.
İlk denklemde a yerine 1 yazıp b değerini bulalım.
7 - 3b = 10
- 3b = 3
b = -1 olur.
c) Her iki denklemi de tek bir paydada yazarak başlayalım işlemimizi yapmaya.
(3x + 2y)/6 = -1 yani;
3x + 2y = -6
(4x - 3y)/6 = 10 yani;
4x - 3y = 60
Yeni denklemlerimizi alt alta yazalım ve uygun sayılarla genişletelim. Yeni sayılarımızı toplayıp bilinmeyen değerlerimizi bulalım.
3x + 2y = -6
4x - 3y = 60
İlk denklem 3 ile ikinci denklem 2 ile genişletilir.
9x + 6y = -18
8x - 6y = 120
17x = 102
x = 6
Oluşturduğumuz denklemlerin birinde x yerine 6 yazalım ve y değerini bulalım.
18 + 2y = -6
2y = -24
y = -12
ç) Bu soruyu çözmek için biraz önceki yöntemlerden yararlanırsak işlemlerimiz çok uzar ve yorucu bir hal alır. Çok daha basit bir şekilde çözmek için sonuçları birbirine eşitleriz. İlk denklemimizin sonucu -11 ve ikinci denklemin sonucu 22'dir. İlk denklemi -2 ile çarparsak ikinci denklem ile eşit olur. Sonra da her iki denklemi birbiri ile eşitleriz.
-2 / (x + 1) +4y = x / (x+1) + 4y
Bu iki denklemde 4y değerleri birbirini götürür. x de karşı denklemde bulunan -2 sayısı ile eşittir. Bize soruda verilen denklemlerde x yerine -2 yazalım ve y değerini bulalım.
1 / (-2 + 1) - 2y = -11
-1 -2y = -11
-2y = -10
y = 5
3. 3x + 4y = 78 denkleminin çözüm kümesinin elemanlarından biri (a-1 , a+1) ise a değerini bulunuz.
Denklemin çözüm kümesi elemanları bize soruda verilmiş. x yerine a-1 ve y yerine a+1 yazarak işlemimizi yapalım.
3 (a - 1) + 4 (a + 1) = 78
3a - 3 + 4a + 4 = 78
7a +1 = 78
7a = 77
a = 11
4.- 2x + 5y = -3, (m - 2).x + 2y = n - 2 denklem sisteminin çözüm kümesi sonsuz elemanlı ise m.n değerini bulunuz.
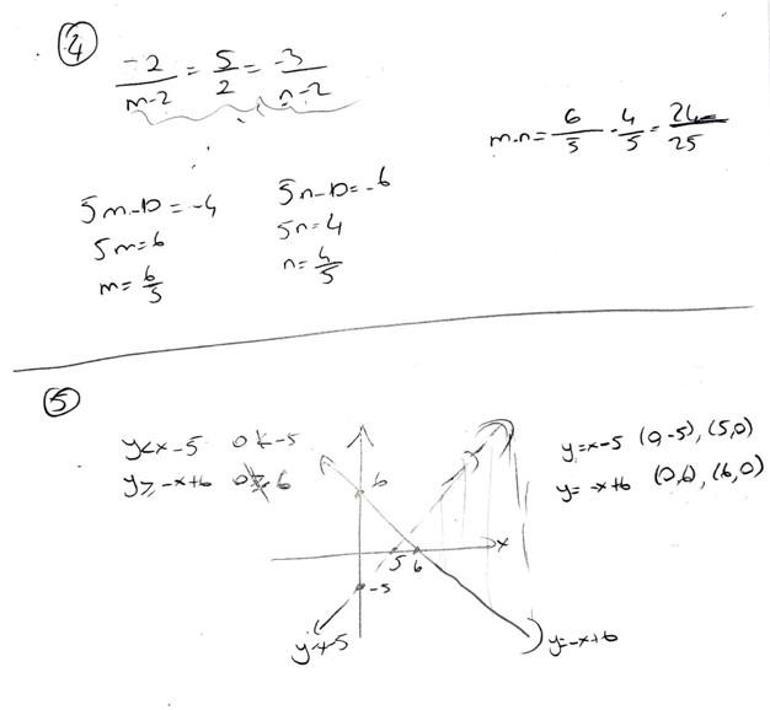
5. y < x - 5, y ≥ -x + 6 eşitsizlik sisteminin çözüm kümesinin elemanlarını analitik düzlemde gösteriniz.
6. Toplamları en çok 6, farkları en az -2 olan gerçek sayı ikililerini analitik düzlemde gösteriniz.
İki sayımızdan biri '' x '' diğeri ise '' y ''olsun.Verilenleri denklem kurarak çözelim.Toplamları en çok 6 demiş x+y = 6 deriz.Farkları en az x-y = -2 deriz.Taraf tarafa toplama yaparsak :
x+y= 6
x-y= -2
-----------
2x = 4
x= 2 olur. Bulduğumuz değerini yerine yazalım :
2+y = 6
y= 4 olur.
7. -5x + y > 10, x ≤ -2 eşitsizlik sisteminin çözüm kümesini analitik düzlemde gösteriniz.
Soruda bize iki tane eşitsizlik sistemi verilmiş. İkinci eşitsizlik sayesinde x'in alabileceği değerleri görebiliriz.
İlk eşitsizlikte x yerine alabileceği en büyük değeri yazarak başlayalım.
x = -2 için
10+y>10
y>0
Bir sonraki en büyük tam sayıyı yazalım. Böylece eşitsizliği hangi y değeri sağlar bunu öğrenmiş olacağız.
x = -3
15+y>10
y>-5
Bu iki x değeri sayesinde anlarız ki x'in en büyük olduğu noktada y, 0'dan büyük bir sayıdır. x sayısı küçüldükçe y sayısı da küçülecektir. x sayısının sonsuza kadar küçüldüğünü de eşitsizlikte bize bir uç değer vermediğinden anlayabiliriz. Bu demek oluyor ki x sayısı sonsuza kadar küçülüyorsa, bu sayıya karşılık gelen y sayısı da sonsuza kadar küçülür.
Kısaca toparlayalım. Eşitsizlikte bize verilen x sayısı sonsuzdan gelip -2'de maksimum değeri alır. x sayısına karşılık gelen y değeri de sonsuzdan gelir 0'dan büyük bir değer alır.
8. |x + y| < 3 eşitsizliğinin çözüm kümesini analitik düzlemde gösteriniz.
(a ∈ R+ , | x | < a ise -a < x < a olduğunu hatırlayınız. )
Doğruların denklemi yazdığında x+y nin her zaman -3 ten büyük 3 den küçük olduğu görülecektir.
x/3+y/3=1
-x/3+-y/3=1
9. Sınıf Matematik Ders Kitabı Sayfa 147 Cevapları
1. Aşağıdaki soruları cevaplandırınız.
a) 2x-1= a ise 4x+1in a cinsinden eşitini bulunuz.
b) (-23 )4 . (-2 )-3 / (-2-2)3. (-2 -1) işleminin sonucunu bulunuz.
c) a = 2(42) ve (24)3 ise a/b ifadesinin eşitini bulunuz.
ç) x ve y , 0 dan farklı gerçek sayılardır. (x3)4 . (y6)3 / (x2 . y4)5 işleminin sonucunu en sade hâlde yazınız.
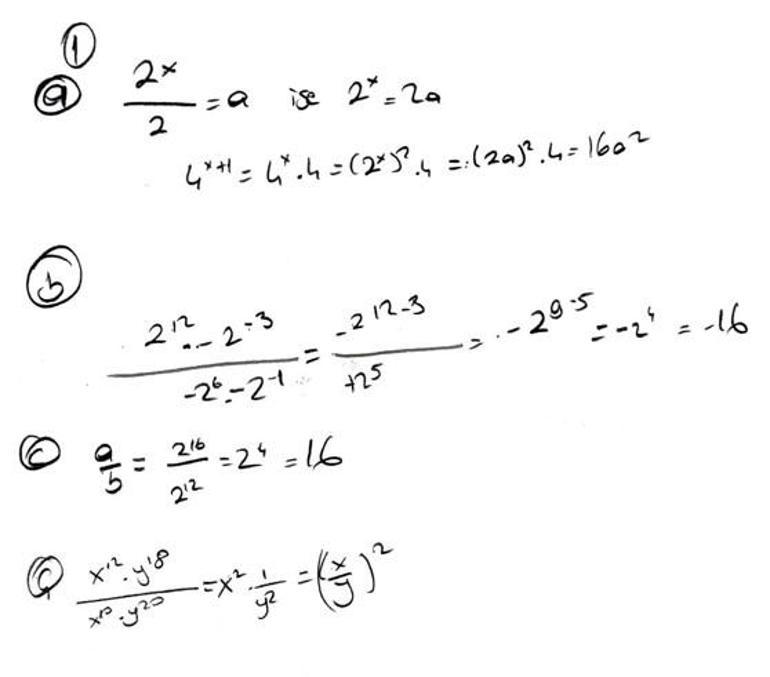
2. a ve b birer tam sayı olmak üzere 74a-2b-4= 6a-5b+8ise a + b toplamını bulunuz.
3. a = 4x+ 3 ve b = (1/2)-2x-3 olarak veriliyor. a nın b cinsinden eşitini bulunuz.
4. ax ≠ 1 olmak üzere (11 / ax– 1) + (11/ a-x – 1) işleminin sonucunu bulunuz.

5. 2 . 4a+1/ 8a+1= 1/4 denkleminin çözüm kümesini bulunuz.
6. (x-4)2x-8= 1 denkleminin çözüm kümesini bulunuz.

7. x, y, z ∈ R olmak üzere
x4∙ y3∙ z5 < 0
y5 ∙ z4 > 0
x3 ∙ z < 0 yukarıda verilenlere göre aşağıdaki eşitsizliklerden doğru olanın yanına (D), yanlış olanın yanına (Y) yazınız.
l. y < 0 dır. (Y)
ll. x < 0 dır. (Y)
lll. z > 0 dır. (Y)
lV. x ∙ y > 0 dır. (D)
V. x/y > 0 dır. (D)
8. 8110+ 2714= a ∙ 920 denklemini sağlayan a sayısını bulunuz.
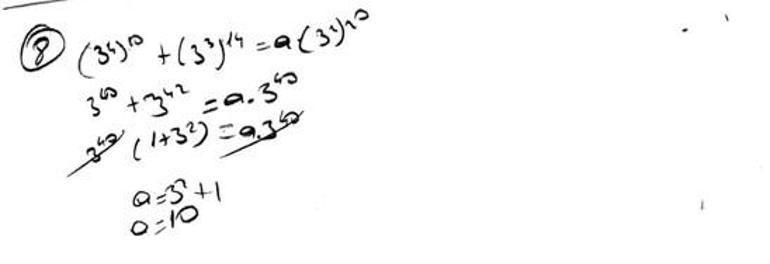
9. 3 ∙ 2a= x veriliyor. 9 ∙ 16aifadesinin x cinsinden eşitini bulunuz.
10. (2 – x / 5)3+ 8 = 0 denkleminin çözüm kümesini bulunuz.
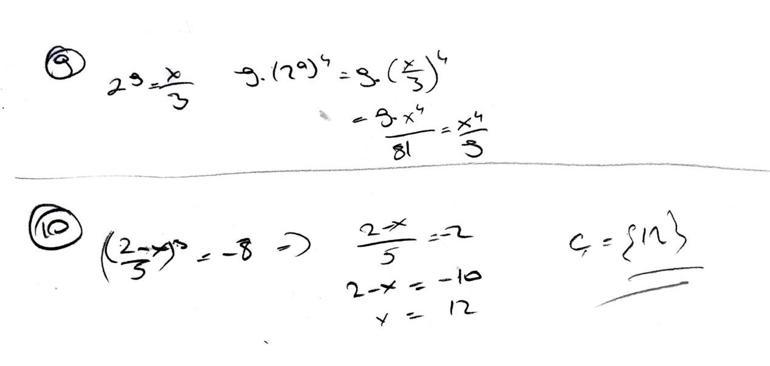
9. Sınıf Matematik Ders Kitabı Sayfa 154 Cevapları
1. √2 ,7 + √0,3 / √1,2 işleminin sonucunu bulunuz.
Çözüm:
√27/10 + √3/10 / √12/10 (paydalar aynı olduğu için kök 10 ları yazmayabiliriz)
√27 + √3 / √12
3√3 + √3 / 2√3
4√3 / 2√3 = 2
2. a = √5 ise ( a - 8 ) . ( a + 2 ) / 4 işleminin sonucunu bulunuz.
Çözüm:
(√5+3-8) . (√5+3+2) / 4
√5-5 . √5+5 / 4
(a-b).(a+b) = a2-b2
5-25 / 4 = -20 / 4 = -5
3. √2 + 1 / √2 / √2 - 1 / √2 işleminin sonucunu bulunuz.
Çözüm:
Paydaki kökden kurtalalım.
1/√2 (√2) ile kökten kurtarırsak
√2 / 2 olur 1/√2 yazan yerlere √2 / 2 yazalım
√2 /1 + √2/2 / √2 / 1 - √2 /2
payda eşitlersek
2√2 +√2 / 2√2 - √2
3√2 / √2 kökler sadeleşirse
3
4. √6 - | x - 2 | sayısının bir gerçek sayı olabilmesi için x tam sayısının kaç farklı değer alabileceğini bulunuz.
5. ∛5 . √5 / ⁴√5 = 5ˣ ise x değerini bulunuz.

6. ∛16ˣ⁺¹ / ∛8ˣ⁻¹ = 4 denkleminin çözüm kümesini bulunuz.
Çözüm:
∛24(x+1) / ∛23(x-1) = 22
∛24x+4 / ∛23x-3 = 22
4x+4 - 3x+3 =x + 7
∛2x+7 = 2 (x+7)/3 =22
x + 7 / 3 = 2
x + 7 = 6
x = -1
Ç= {-1}
7. a < b < 0 ve a, b ∈ R olmak üzere √( a - b )² - ∛ ( b - a )³ - ⁴√a⁴ işleminin sonucunu bulunuz.
Çözüm:
√8 + √60 - √8 - √60 işleminin sonucunu bulunuz.
⁴√³√x = ³√9 . ⁴√3 olduğuna göre x in değerini bulunuz.
a = -√3
b = -∛6 sayılarını küçükten büyüğe sıralayınız.
c = -⁶√20
8. √8 + √60 - √8 - √60 işleminin sonucunu bulunuz.
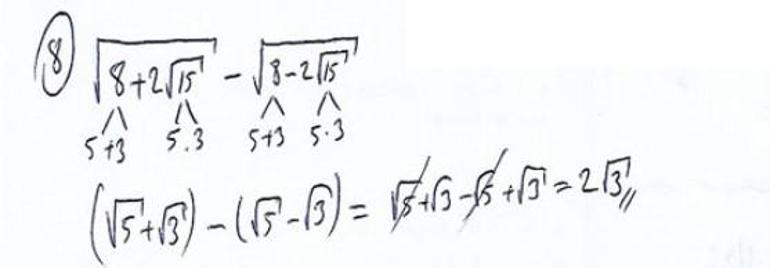
9. ⁴√³√x = ³√9 . ⁴√3 olduğuna göre x in değerini bulunuz.
10. a = -√3
b = -∛6 sayılarını küçükten büyüğe sıralayınız.
c = -⁶√20
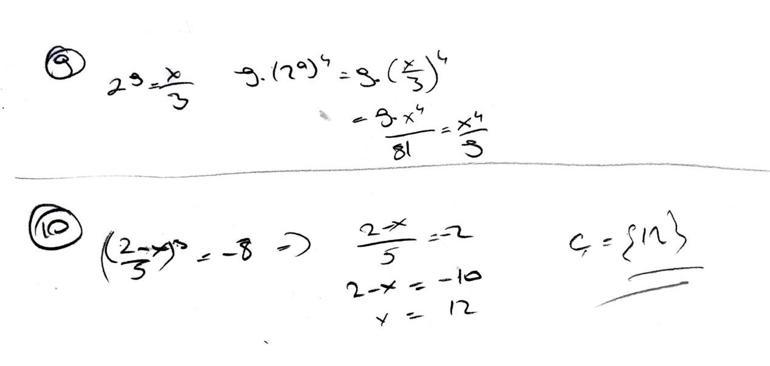
9. Sınıf Matematik Ders Kitabı Sayfa 161 Cevapları
1. x/y = 3/8 ve y - x = 20 ise x değerini bulunuz.
Çözüm:
x/y = 3/8 verilmiş. İçler dışlar çarpımından birbirlerine eşitleyelim.
3x = 8y olur. Yani, 3x-8y = 0
3x-8y = 0
y-x = 20 denklemlerini alt alta toplayalım. İkinci denklemin her elemanını 3 ile çarparsak x'li ifadeler birbirini götürecektir.
3x-8y = 0
3y-3x = 60
-8y+3y = 60
-5y = 60
y = 60/-5
y = -12
y-x denkleminde y'yi yerine yazarsak x'e ulaşırız.
-12-x = 20
-12-20 = x
-32 = x
2. a/b = 3/5 ve b/c = 2 ise a/c değerini bulunuz.
Çözüm:
Soruda bize b/c = 2 olarak verilmiş. Bu ifadeden b=2c olarak bulunur. Şimdi bize verilen ilk denklemde b gördüğümüz yere 2c yazarsak a/c değerini bulabiliriz.
a/2c = 3/5 sonucuna ulaştık.
Şimdi a/c'yi elde etmek için eşitliğin her iki tarafını da 2 ile çarparız.
a/c = 6/5
3. (2m + n)/(m-n) = 4 ise m²/n² değerini bulunuz.
Çözüm:
(2m+n)/(m-n)=4 olarak verilmiş. Biz bu denklemden;
2m+n = 4(m-n) elde edebiliriz.
2m+n = 4m-4n
2m = 5n olarak buluruz.Elimizdeki iki bilinmeyenden kurtulmak için m ve n yerine tek bir değer yazalım.
m = 5k ve n = 2k yazarsak denklemimiz doğru olacaktır.
Şimdi de son olarak m²/n² yerine değerlerimizi yazalım.
25k²/4k² bilinmeyen değerler sadeleşir ve geriye yalnızca 25/4 kalır.
4. Bir sınıftaki kız öğrencilerin sayısı 0,24 ile erkek öğrencilerin sayısı 0,36 ile doğru orantılıdır. Sınıf mevcudu 30 dan fazla olduğuna göre sınıf mevcudunun en az kaç olabileceğini bulunuz.
Çözüm:
Sınıftaki kız sayısı 0,24 ile orantılıysa bunu bir k değişkeni ile ifade etmeliyiz. Orantılı olma ifadesi doğru orantılı olmayı ifade ettiğine göre,
Kız öğrenci sayısı= 0,24k
Bu durumda erkek öğrenci sayısı= 0,36k
Öyleyse toplam sınıf mevcudu= 0,24k+0,36k= 0,60k bulunur.
Sınıf mevcudu 30'dan fazla ise eşitsizliğimizi yazalım.
0,60k> 30
k>50 bulunur. Ancak sınıf mevcudu bir tamsayı olabilir ve negatif olamaz. Bu durumda 0,60k= 60k/100 ifadesi ancak 100 ile sadeleşebilecek bir k sayısı olmalıdır. Bu durumda 50'den büyük olan ve 100 ile sadeleşebilecek tek sayı 55 olacaktır. Öyleyse:
(60*55)/100= 33 kişi olabilirler.
5. Akif ve Mert bir arsayı 2/5 oranında hisse ile almak istemektedir. Küçük hisseyi Akif 32.000 TL karşılığında aldığına göre arsanın tamamının kaç TL olduğunu bulunuz.
Çözüm:
Akif'in hissesine 2k dersek Mert'in hissesi 5k olacaktır. Küçük olan hisse yani Akif'in hissesi 32000 TL olduğuna göre:
2k = 32000 ise k = 16000 TL'dir.
k = 16000 ise 5k = 5 x 16000 = 80000 TL (Akif'in hissesi)
Arsanın tamamı=32000 + 80000 = 112000 TL
6. a sayısı b+1 ile doğru, c-2 ile ters orantılıdır. a = 5 ve b = 2 iken c = 8 ise b = 3 ve c = 4 iken a değerini bulunuz.
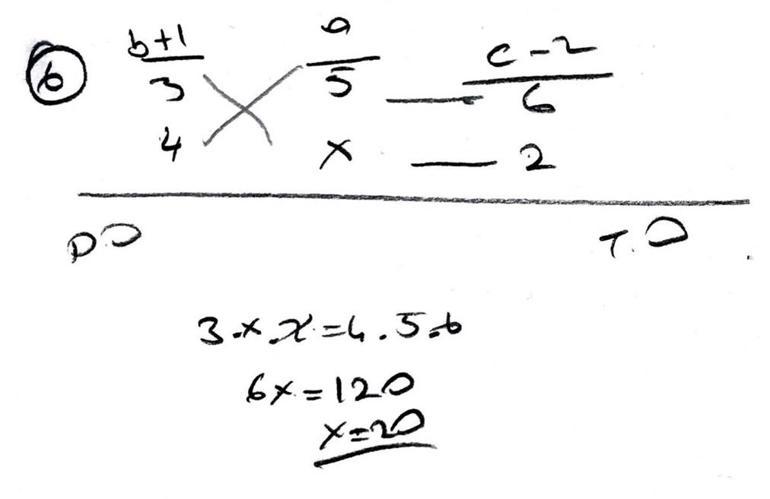
7. Özdeş olan 25 adet güneş panelinin 12 günde ürettiği elektriği , aynı şartlarda bu panellerle özdeş ve 3 kat daha fazla sayıdaki güneş paneli ile kaç günde üretebileceğini bulunuz.
Çözüm:
Bu soru ters orantı kurularak çözülür.Çünkü güneş paneli sayısıyla gün birbirine ters orantılıdır.Güneş paneli sayısı arttıkça daha çok elektrik üretileceği için,aynı miktarda elektrik daha az günde üretilir.
25 adet 12 gün
75 adet x gün
25.12 / 75 =x = 4 günde üretilir.
Aslında buna 75 bile demeden direkt olarak güneş paneli sayısı 3 kat artacaksa gün sayısı da 3 e bölünecek diyebilirdik.
8. Cennet Hanım anaokuluna giden kızı ile hafta sonu kek yapmak istemektedir. Bunun için gerekli olan un, şeker ve tereyağı miktarları sırasıyla 8, 3 ve 2 sayıları ile doğru orantılıdır. Cennet Hanım ve kızının yaptığı 4 kişilik bir kek 1300 gr olduğuna göre yapacakları 8 kişilik bir kekte kaç gram tereyağı kullanacaklarını bulunuz.
Çözüm:
Soruda verilenlere göre kekin içindeki malzemelerin oranı şu şekildeymiş;
Un : 8 k
Şeker : 3 k
Tereyağı: 2 k
toplamda: 8k + 3k + 2k = 13 k malzeme bulunuyor.
4 kişilik kek 1300 gr ise ⇒ 8 kişilik kek: 1300 gr x 2 = 2600 gr olur.
toplamda malzemeler 13 k olduğuna göre
13 k = 2600 gr
k =200 gr olur.
Tereyağ miktarı 2k ise 200 x 2 = 400 gram tereyağı bulunur.
9. Bir bilim insanı demir, alüminyum ve kurşun metallerini sırasıyla 3, 4 ve 12 sayıları ile ters orantılı olacak şekilde karıştırıp 240 gramlık bir alaşım elde ediyor. Bu alaşımdaki alüminyum miktarını bulunuz.
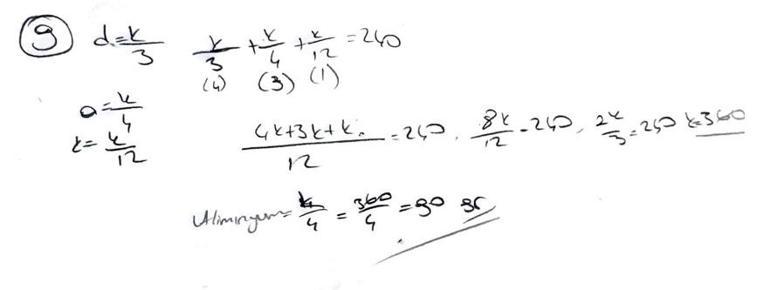
10. Bir uçak firması bilet fiyatlarını 30 boş koltuk kalana kadar sabit bir fiyatla boş koltuk sayısı 30 un altına düştüğünde koltuk sayısı ile ters orantılı olacak şekilde belirlemektedir. 20 boş koltuğu olan bir uçakta bilet fiyatı 75 TL ise 15 boş koltuk kaldığında bilet fiyatının kaç TL olacağını bulunuz.
Çözüm:
Koltuk sayısı 30'un altına düştüğünde fiyat koltuk sayısı ile ters orantılı olarak belirlendiğine göre:
x/20=75==>x/15=? (soru bu hale geldi)
x=20x75=1500==>x/15=1500/15=100
Bilet fiyatı 100TL olmalı.
9. Sınıf Matematik Ders Kitabı Sayfa 182-183 Cevapları
1. Toplamları 24 olan iki sayıdan birinin 3 katı diğerinin 5 katına eşittir. Buna göre küçük sayıyı bulunuz.
Çözüm :
K = 3X
B = 5X
8X = 24 => X = 3
K = 3X = 3 x 3 = 9
2. Selim’in parası Selin’in parasının 4 katıdır. Selim Selin’e 54 TL verirse paraları eşit olur. Buna göre Selin’in ilk durumdaki parasının kaç TL olduğunu bulunuz.
Çözüm :
Selim / 4X
Selin / X
4X - 54 = X + 54
3X = 108
X = 36
3. Bir çay bahçesinde 3 veya 4 kişilik toplam 20 masa vardır. Çay bahçesinin kapasitesi 74 kişi olduğuna göre 4 kişilik masa sayısını bulunuz.
Çözüm :
4 Kişilik / X
3 Kişilik / 20 - X
4X + 3 (20 - X) = 74
4X + 60 - 3X = 74
X = 14
4. Bir manav elindeki limonların birinci gün 1/4'ünü, ikinci gün ise kalan limonların 1/5'ini satmıştır. Geriye 48 kg limonu kaldığına göre toplam kaçkg limon sattığını bulunuz.
Çözüm :
Limon sayısı 20X oldun
gün 20X . 1 /4 = 5X satıldı
Kalan 20X - 5X = 15X
gün 15X . 1/5 = 3X satıldı
Kalan 15X - 3X = 12X
12X = 48 => X = 4
Satılan 5X + 3X = 8X = 8 x 4 = 32
5. Şenol Bey eve internet bağlatmak için 4 GB lık veri indirme ücreti 6 TL olan bir firma ile anlaşıyor. Şenol Bey, bir ayda 38 GB lık indirme yaparsaŞenol Bey’in ay sonundaki fatura tutarının kaç TL olacağını bulunuz.
Çözüm :
4 GB 6 TL
38 GB X TL işler dışlar çarpımı ile
X = 38 x 6 / 4 = 57 TL
6. Pazarda öğleden önce 3 kg patatesi 5 TL ye satan bir pazarcı, öğleden sonra 4 kg patatesi 5 TL ye satmaya başlıyor. Buna göre pazarcının ilk satış fiyatına göre yüzde kaç indirim yaptığını bulunuz.
Çözüm :
Öğleden sonra 1 kg 5/4 TL
İndirim Miktarı 5 / 3 - 5 / 4 payda eşitlersek 12'de
20 - 15 / 12 = 5 / 12 olur
5 / 3 te 5 / 12 indirim
100 X
5 / 3X = 100 X 5 / 12
X = 100 / 4 = 25 => % 25 indiirm
7. Bir ürün alış fiyatı üzerinden %20 kârla satılırken satış fiyatı üzerinden %20 zamla 360 TL ye satılıyor. Buna göre ürünün alış fiyatını bulunuz.
Çözüm :
Alış fiyatı 100X
Satış fiyatı 120X
Karlı satış fiyatı 120X . 120 / 100 => 144 X = 360
X = 360 / 144 = 5 / 2
Alış fiyatı = 100X = 100 x 5 / 2
X = 250 TL
8. Bir tüccar X tanesini Y liraya aldığı bir ürünün tanesini Z liradan satmaktadır. Tüccar bu satıştan ne kâr ne de zarar ettiğine göre X, Y ve Z arasındaki bağıntıyı bulunuz.
Çözüm :
Y / X = Z
Y = X . Z
9. Nazan ile Numan’ın yaşları toplamı 28 dir.Eğer Nazan 4 yıl önce, Numan ise 5 yıl sonra doğmuş olsaydı Numan’ın yaşı Nazan’ın yaşından 3 fazlaolacaktı. Buna göre Nazan’ın şimdiki yaşını bulunuz.
Çözüm :
Nazan - Şimdi X olsun, 4 yıl sonra X + 4 olur
Numan - Şimdi 28 - X, 5 yıl sonra 23 - X olur
X + 4 + 3 = 23 - X
X + 7 = 23 - X
2X = 16
X = 8 olur
10. Bayan çantası satan bir mağaza alış fiyatı üzerine %30 kâr payı ekleyerek etiket fiyatını belirlemektedir. Sezon sonu ise etiket fiyatı üzerinden %30 indirim yaparak satış yapmaktadır. Sezon sonunda maliyetinden 18 TL daha düşük fiyata satılan bir çantanın alış fiyatının kaç TL olduğunu bulunuz.
Çözüm :
Alış 100X
%30 karla 130X
İndirimli fiyatı 130X . 70 / 100 = 91X
100X - 91X = 18
9X = 18
X = 2
Alış fiyatı 100 x 2 = 200
11. %40 ı şeker olan 120 litre şekerli suyun yarısı ile %20 si şeker olan 100 litre şekerli suyun 5 2 i karıştırılıyor. Son durumda karışımın şeker oranının yüzde kaç olacağını bulunuz.
Çözüm :
60 . 40 / 100 = 24 şeker
100 . 2 / 5 = 40 lt
40 . 20 / 100 = 8 şeker
Toplam karışım (24 + 8) / (60 + 40) = 32 / 100 = %32
12. Bir araç hızını saatte 30 km arttırırsa bir yolu 4 saatte, hızını saatte 20 km azaltırsa aynı yolu 6 saatte almaktadır. Buna göre bu aracın hızını değiştirmeden bu yolu kaç saatte alacağını bulunuz.
Çözüm :
X = v . t
(v + 30) . 4 = (v - 20) . 6
4v + 120 = 6v - 120
2v = 240
v = 120
x = (v +30) . 4 = (120 + 30) .4 = 600 km
13. Yandaki grafikte A, B ve C kaplarındaki şeker ve su miktarları verilmiştir. Bu kaplardan eşit miktarda karışımlar alınıp yeni bir kaba dökülürse oluşan karışımın şeker oranının yüzde kaç olacağını bulunuz.
(2 + 4 +6) / (10 + 10 + 10) = 12 / 30 = 4 / 10 = 40 / 100 => % 40
15. Şekildeki dairesel pistte V1=30 m/sn. ve V2=20 m/sn. hızlarıyla iki araç aynı anda birbirine doğru hareket ettikten 4 sn. sonra ilk kez karşılaşıyorlar. Bu araçlar hiç durmadan yollarına devam ettiklerinde 11. kez karşılaşmalarının harekete başlamalarından kaç saniye sonra gerçekleşeceğini bulunuz.
X = (V1 + V2) . t
(30 + 20) . 4 = 200 m
Pistin tamamı 200 . 360 / 120 = 600 m
600 = (30 + 20) . t
t = 12 sn
12 . 10 + 4 = 124 sn
16. Hızları saatte 80 km ve 60 km olan iki araç aynı anda aynı noktadan aynı yolu kullanarak aynı yere gittiklerinde, hızlı araç yavaş olan araçtan 2 saat önce varmaktadır. Buna göre yavaş olan aracın bu yolu kaç saatte gittiğini bulunuz.
80 . t = 60. (t + 2)
80t = 60t + 120
20t = 120
t = 6
Yavaş olan t + 2 = 6 + 2 = 8 saat
17. Bir karışımdaki şeker miktarının su miktarına oranı 17 8 dir. Buna göre karışımdaki şeker oranının yüzde kaç olduğunu bulunuz.
Karışım = Şeker + su = 8 + 17 = 25
25 8
100 X
X = % 32 olur
18. Bataryaları boş olan A ve B marka cep telefonlarının şarj olma süreleri sırasıyla 4 ve 5 saattir. A marka telefonun %20 si, B marka telefonun %10 u dolu iken aynı anda şarja takılan bu telefonlardan A marka telefonun bataryası %100 dolduğunda B marka telefonun bataryasının yüzde kaç dolmuş olacağını bulunuz.
4 saat 100
x 80
x = 32 /10 saat
5 saat 100
32/10 saat x
x = % 72
19. Şekilde A ve B araçlarının yol-zaman grafiği verilmiştir. Bu araçların aynı anda aralarında 800 km olan iki noktadan birbirine doğru hareket ettikten kaç saat sonra karşılaşacaklarını bulunuz.
20. Bir ayda 200 kilovat elektrik tüketen bir haneye ay sonunda 100 lira fatura gelmiştir. Bu faturadaki vergi miktarı, tüketilen elektrik tutarının %25 i kadardır. Buna göre 1 kilovat elektriğin fiyatı kaç liradır?

9. Sınıf Matematik Ders Kitabı Sayfa 184-194 Cevapları
1. M ve N birer küme olmak üzere M = (-5, 4] ve N = [1, ∞) olarak veriliyor. Buna göre M – N kümesi aşağıdakilerden hangisidir?
A)(-5, 1]
B)(-5, 1)
C) (-5, ~)
D) (-5, 2)
E) [-5, 2]
Cevap: B
2. (2x – 4) + 8 = 3 . (4x – 4) – 4 denkleminin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir?
A){0}
B){ }
C) R
D) {4}
E) {-4}
Cevap: C
3. 2 + 20 / 3 + 12 / x – 1 = 6 denklemini sağlayan x değeri aşağıdakilerden hangisidir?
A)4
B)5
C) 6
D) 7
E) 8
Cevap: D
4. (x + 4 / x – 2) + (x – 5 / x +3) = (x + 4 / x – 2) + 3 / 4 denklemini sağlayan x değeri aşağıdakilerden hangisidir?
A)30
B)28
C) 29
D) 27
E) 26
Cevap: C
5. M ve N birer doğal sayıdır. Yukarıdaki bölme işlemlerine göre M sayısı kaçtır?
A)32
B)41
C) 56
D) 78
E) 99
Cevap: A
6. AB iki basamaklı doğal sayısının A+B toplamına bölümünde bölüm 4, kalan 3 olduğuna göre kaç farklı AB yazılabilir?
A)2
B)3
C) 4
D) 5
E) 6
Cevap: C
7. Aşağıdaki sayılardan hangisi 2, 3 ve 4 ile tam bölünür?
A)145
B)242
C) 366
D) 456
E) 632
Cevap: D
8. 23 basamaklı 4242…4 sayısının 9 ile bölümünden kalan kaçtır?
A)0
B)1
C) 3
D) 4
E) 7
Cevap: E
9. Beş basamaklı 4x56y sayısının hem 3 hem de 5 ile bölümünden kalan 2 olduğuna göre x + y toplamı aşağıdakilerden hangisi olamaz?
A)2
B)5
C) 8
D) 11
E) 15
Cevap: E
10. x4yz ve x7yz dört basamaklı birer doğal sayıdır. x4yz sayısının 11 ile bölümünden kalan 4 olduğuna göre x7yz sayısının 11 ile bölümünden kalan kaçtır?
A)4
B)5
C) 7
D) 9
E) 11
Cevap: C
11. Bir A doğal sayısı 15 ile bölündüğünde bölüm x, kalan 9 dur. x doğal sayısının 4 ile bölümünden kalan 1 dir. Buna göre A doğal sayısının 12 ile bölümünden kalan kaçtır?
A)0
B)3
C) 7
D) 9
E) 10
Cevap: A
12. 6 ya, 8 e ve 9 a bölündüğünde 4 kalanını veren en küçük iki basamaklı doğal sayı aşağıdakilerden hangisine tam olarak bölünür?
A)7
B)13
C) 16
D) 19
E) 23
Cevap: D
13. Yaşar’ın 2 bilyesi daha olsaydı bilyeleri dörderli, beşerli ve altışarlı gruplara ayrılabilecekti. Buna göre Yaşar’ın bilyelerinin sayısı aşağıdakilerden hangisi olabilir?
A)120
B)182
C) 238
D) 302
E) 404
Cevap: C
14. Bir marangoz boyutları 48 cm, 72 cm, x cm olan dikdörtgenler prizması şeklindeki tahta bloğu eş küplere ayırmıştır. Toplam 168 tane eş küp elde ettiğine göre x en az kaçtır?
A)80
B)84
C) 88
D) 96
E) 168
Cevap: B
15. Lacivert ve sarı eş kareler kullanılarak şekildeki gibi süsleme yapılmıştır. Bu süslemede 55 lacivert kare olduğuna göre kaç tane sarı kare vardır?
A)110
B)125
C) 150
D) 165
E) 175
Cevap: D
16. Ada ve Ata iki farklı şehirde yaşamakta olan iki kardeştir. Ada 15 günde bir, Ata ise 20 günde bir ailelerini ziyarete gelmektedirler. İki kardeş ilk kez cumartesi günü birlikte ailelerini ziyaret ettiklerine göre 5. kez ailelerini hangi gün birlikte ziyaret ederler?
A)Perşembe
B)Cuma
C) Cumartesi
D) Pazar
E) Pazartesi
Cevap: E
17. 123454321234543212345… şeklinde her beş rakamda bir tekrar eden sayının soldan 500. basamağındaki rakam kaçtır?
A)1
B)2
C) 3
D) 4
E) 5
Cevap: D
18. Aynı hastanede görev yapan Dr. Sevilay Hanım 8 günde bir, Hemşire Gülay Hanım ise 5 günde bir nöbet tutmaktadır. İkisi birlikte ilk nöbetlerini salı günü tuttuklarına göre 11. nöbetlerini birlikte hangi gün tutarlar?
A)Pazartesi
B)Salı
C) Çarşamba
D) Perşembe
E) Cuma
Cevap: C
19. 3 – m / 2 ≤ 2m + 4 / 3 eşitsizliğini sağlayan m tam sayısının en küçük değeri kaçtır?
A)-2
B)-1
C) 0
D) 1
E) 2
Cevap: D
20. x – 1 ≤ 3 – x < 7 + 3x eşitsizliğini sağlayan x gerçek sayılarının aralığı aşağıdakilerden hangisidir?
A)(-1,2]
B)(1, 2)
C) (-2, -1]
D) [-1, 2)
E) [-2, -1)
Cevap: A
21. ” Sayı doğrusu üzerinde 7 sayısına uzaklığı en az 10 birim olan gerçek sayılar” ifadesi aşağıdakiler- den hangisinde doğru olarak belirtilmiştir?
A)|x – 7| > 10
B)|x – 10| > 7
C) |x – 7| < 10
D) |x – 7| ≤ 10
E) |x – 7| > 10
Cevap: E
22. x e R+olmak üzere 1/32 ≤ 1 / 4x + 4 < 1/16 eşitsizliğinin gerçek sayılardaki çözüm kümesi aşağıdakiler- den hangisidir?
A)(4, 7]
B) [4, 7)
C) [3, 7]
D) [3, 7)
E) (3, 7]
Cevap: E
23. a, b, c birer negatif tam sayıdır. a / b+ c < a / a + c olduğuna göre aşağıdakilerden hangisi daima doğrudur?
A)a > c
B)a < c
C) a > b
D) b > a
E) b > c
Cevap: D
24. 2 < x < y < 4 eşitsizliği veriliyor. Buna göre 3x – 2y ifadesinin alabileceği en küçük tam sayı değeri aşağıdakilerden hangisidir?
A)-5
B)-4
C) -3
D) -2
E) -1
Cevap: E
25. | x-1 / 30| = 20172017denklemini sağlayan x değerleri toplamı kaçtır?
A)3
B) 2
C) 1
D) 0
E) -1
Cevap: B
26. |1 / 3-a | = 2 denklemini sağlayan a değerleri toplamı kaçtır?
A)-2
B)0
C) 3
D) 4
E) 6
Cevap: E
27. 4x + |3x| – 21 = 0 denkleminin çözüm kümesi aşağıdakilerden hangisidir?
A){3}
B){21}
C) {3,21}
D) Ø
E) R
Cevap: A
28. a, b, A ∈ R olmak üzere A = |3a – 2b| olarak veriliyor. A nın en küçük değeri için 5a – 2b / b – a işleminin sonucu kaçtır?
A)-4
B)-2
C) 0
D) 2
E) 4
29. x, y, z ∈ R+ olmak üzere 1/x < 1/y < 1/z ise | x – y | + | y – z | + | x – z| toplamı aşağıdakilerden hangisidir?
A) 2x – 2z
B) 2x – 2y
C) 2y – 2x
D) 2y – 2
E) 2z – 2x
Cevap: A
30. a ve b birer gerçek sayıdır. Buna göre
l. |a . b| = | a | . | b|
ll. |a . b| = |a . b|
III. |ab|= |a|b
IV. |a-b| = |b-a|
ifadelerinin hangileri daima doğrudur?
A) I, III
B) I, III
C) I, IV
D) II, IV
E) I, II, IV
Cevap: C
31. m, n ∈ R olmak üzere |x – 3| < m eşitsizliğinin çözüm kümesi (-5, n) olduğuna göre m+n aşağıdakilerden hangisidir?
A) 2
B) 5
C) 9
D) 16
E) 19
Cevap: E
32. 1 ≤ |x – 4| < 3 eşitsizliğini sağlayan x tam sayılarının toplamı aşağıdakilerden hangisidir?
A) 16
B) 15
C) 14
D) 13
E) 12
Cevap: A
33. x, y ∈ R olmak üzere |x – 6| < 2 ve |y + 1| < 2x tür. Buna göre x + y nin en büyük tam sayı değeri kaçtır?
A) 18
B) 19
C) 20
D) 21
E) 22
Cevap: E
34. |x – 4 / x + 6| + 6 ≤ 0 eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
A) (6, ∞)
B) (-6, ∞)
C) (-∞, 6)
D) (-∞,- 6)
E) Ø
Cevap: E
35. ax – by = 11, (a + 1) . x + (b – 4) . y = 8 denklem sisteminin çözüm kümesi (3, -1) sıralı ikilisi olduğuna göre a + b toplamı kaçtır?
A) 3
B) 4
C) 5
D) 6
E) 7
Cevap: E
36. |4x – y + 3| + |x + y + 12| = 0 denklemini sağlayan x ve y değerlerinin çarpımı aşağıdakilerden hangisidir?
A) -9
B) -6
C) -3
D) 18
E) 27
Cevap: E
37. ax + 9y – 1 = 0, 4x + ay – 5 = 0 denklem sisteminin çözüm kümesi boş küme ise a gerçek sayısının negatif değeri aşağıdakilerden hangisidir?
A) -36
B) -6
C) -3
D) -2
E) -1
Cevap: B
38. A şehrinden C şehrine doğru hareket eden bir araç 120 km sonra B ile C şehrinin orta noktasına, C şehrinden hareket eden bir araç ise 180 km sonra A ile B şehirlerinin orta noktasına ulaştığına göre A ile C şehirlerinin arasındaki uzaklık kaç km dir?
A) 100
B) 200
C) 300
D) 400
E) 500
Cevap: B
39. 7x – 2y = -20, 3x + 4y = 6 ( m + 1)-x + 2y = 0 denklem sisteminin çözüm kümesi aynı (x,y) sıralı ikilisidir. Buna göre m kaçtır?
A) -3
B) -2
C) 0
D) 2
E) 3
Cevap: D
40. 5x + 7y = -1, 3x + 11y = -3 denklem sistemi veriliyor. Buna göre 7x + 3y toplamı aşağıdakilerden hangisidir?
A) -1
B) 0
C) 1
D) 2
E) 3
Cevap: C
41. a, b, c sıfırdan farklı gerçek sayılardır. … ise y + y + y toplamı aşağıdakilerden hangisidir?
A) -1
B) 1
C) 2
D) 4
E) 6
Cevap: B
42. Yukarıdaki boyalı bölge aşağıdaki eşitsizliklerden hangisinin çözüm kümesini belirtmektedir?
A) 4x + 3y > 24
B) 4x + 3y > 24
C) 4x – 3y > 24
D) 4x + 3y < 24
E) 4x + 3y < 24
Cevap: B
43. A={(x,y) | -2 < x + y < 3 , x, y ∈ R } kümesinin elemanları aşağıdaki grafiklerden hangisinde doğru boyanmıştır?
Cevap: C
44. n ∈ R olmak üzere 3n -1 + 2.3n-2 / 2.3n-3 + 3n-2 işleminin sonucu kaçtır?
A) 7
B) 6
C) 5
D) 4
E) 3
Cevap: E
45. 3a= 5, 5b = 2 olduğuna göre 9ab+1 değeri aşağıdakilerden hangisidir?
A) 16
B) 25
C) 27
D) 36
E) 75
Cevap: D
46. 272x-2 = 243x denklemini sağlayan x değeri kaçtır?
A) 2
B) 3
C) 4
D) 5
E) 6
Cevap: E
47. (2x-5)2x 6 – 1 = 0 denklemini sağlayan farklı x değerlerinin toplamı kaçtır?
A) 5
B) 4
C) 3
D) 2
E) 1
Cevap: A
48. 43x . 8x-1 = 162x-1 . 22-3x denklemini sağlayan x değeri aşağıdakilerden hangisidir?
A) 1
B) 2
C) 4
D) 1
E) 4
Cevap: C
49. a ∈ R olmak üzere a0,6 = 64 ise a0,2 değeri aşağıdakilerden hangisidir?
A) 8
B) 4
C) 2
D) 1
E) 1/4
Cevap: B
50. a ve b birer tam sayı olmak üzere 35a-2 . 7a+b = 53 ise b değeri aşağıdakilerden hangisidir?
A) 2
B) 0
C) -3
D) -5
E) -8
Cevap: E
51. 34 + 33 / 9a = 4/3 denklemini sağlayan a değeri aşağıdakilerden hangisidir?
A) 1
B) 2
C) 0
D) -1
E) -2
Cevap: B
52. 1 / 31-a = 2 olduğuna göre 9a değeri aşağıdakiler- 3 den hangisidir?
A) 1/9
B) 1/4
C) 4
D) 9
E) 36
Cevap: E
53. [x4 . (-x-3)4]1/2 / x-7 işleminin sonucu aşağıdakilerden hangisidir?
A) x2
B) x3
C) x4
D) -x3
E) -x4
Cevap: B
54. x,y,k ∈ R ve k ≠ -3/2 olmak üzere x = 53/2k + 3 ve y = 252k/k+3 tır. Buna göre y nin x cinsinden eşiti aşağıdakilerden hangisidir?
A) 5/x
B) 25/x
C) 5/x2
D) 1
E) 5
Cevap: A
55. 34 . 25 + 24 . 35 / 45 işleminin sonucu aşağıdakilerden hangisidir?
A) 108
B) 120
C) 144
D) 180
E) 216
Cevap: C
56. 2x=a, 3x = b, 5x = c olarak veriliyor. Buna göre(0,72)x sayısının a, b, c cinsinden yazılışı aşağıdakilerden hangisidir?
A) a • b2 • c2
B) a • b2 • c-2
C) a • b • c2
D) a2 • b2 • c
E) a2 • b • c-2
Cevap: B
57. 411 + 411 + 411 + 411 / 215 + 215 denklemini sağlayan x değeri aşağıdakilerden hangisidir?
A) 5
B) 6
C) 7
D) 8
E) 9
Cevap: C
58. 4x-6 – 2x-1 > 0 eşitsizliğini sağlayan en küçük x tam sayısı aşağıdakilerden hangisidir?
A) 12
B) 11
C) 10
D) 9
E) 8
Cevap: A
59. (3/5)4x-12 < (27/125)-2x+6 eşitsizliğinin gerçek sayılardaki çözüm kümesi aşağıdakilerden hangisidir?
A) (-∞, 3)
B) (-∞, 3]
C) (3,∞)
D) [3, ∞)
E) (4,∞)
Cevap: C
60. A bir gerçek sayı olmak üzere A = √2x – 12 + 3√x + 2 – 4√6-x olarak verilmiştir. A sayısı aşağıdakilerden hangisidir?
A) -2
B) 0
C) 2
D) 4
E) 6
Cevap: C
61. x = √6 + √2 ve y = √6 – √2 olmak üzere x.y / x+y işleminin sonucu aşağıdakilerden hangisidir?
A) √6/3
B) √6/2
C) √6
D) -√6/2
E) -√6/3
Cevap: A
62. 3√3 . 4√3 = 3√4√x olduğuna göre x gerçek sayısı aşağıdakilerden hangisidir?
A) 314
B) 312
C) 310
D) 37
E) 33
Cevap: D
63. (2 / √2 + √3) + (2 / √2 – √3) işleminin sonucu aşağıdakilerden hangisidir?
A) -2√2
B) -√3
C) √6
D) 2√6
E) √3-1
Cevap: D
64. (6 / 3 + √3) + (6 / 3 – √3) işleminin sonucu aşağıdakilerden hangisidir?
A) 3
B) 6
C) √3
D) 3√3
E) √3 + 3
Cevap: B
65. (1 / 1+(1/√2)) / (1/√2) işleminin sonucu aşağıdakilerden hangisidir?
A) √2
B) √2-1
C) √2 + 1
D) 2√2-1
E) 2√2-2
Cevap: E
66. (√7 + √24 + √7 – √24 )2 işleminin sonucu aşağıdakilerden hangisidir?
A) 6
B) 4√6
C) 12
D) 24
E) 36
Cevap: D
67. 3√3√24 sayısı √3 sayısının kaç katıdır?
A) √2
B) √3
C) 3√4
D) 3√9
E) 3√12
Cevap: A
68. A = √7 – 3 / √13 – 5 ve B = √13 + 5 / √7 + 3 sayıları veriliyor. Buna göre B nin A cinsinden yazılışı aşağıdakilerden hangisinde doğru olarak verilmiştir?
A) B = A
B) B = -A
C) B = 3A
D) B = 3A
E) B = 6A
Cevap: E
69. √(9x+2/27x-1) = 81 eşitliğini sağlayan x gerçek sayısı aşağıdakilerden hangisidir?
A) -5
B) 0
C) 5
D) 10
E) 15
Cevap: A
70. 6√25x = 4√125y olarak verildiğine göre y değeri aşağıdakilerden hangisidir?
A) 4/9
B) 9/4
C) 1/4
D) 1/9
E) 1
Cevap: B
71. 3√( 21 . 212 – 5 . 212 / 26 + 26) işleminin sonucu aşağıdakilerden hangisidir?
A) 1
B) 2
C) 4
D) 8
E) 16
Cevap: D
72. √(√5 – 1) . (√5 + 1) işleminin sonucu aşağıdakilerden hangisidir?
A) 1
B) 42
C) 4
D) 2√5
E) 2
Cevap: E
73. 2√x + 5√y = 16, 3√x – √y = 7 denklem sistemini sağlayan x 34X – 4y = 7 ve y gerçek sayılarının toplamı aşağıdakilerden hangisidir?
A) 4
B) 5
C) 13
D) 17
E) 19
Cevap: C
74. a . x – (a + 2) . y = √500 denkleminin çözüm kümesi ÇK = {(√5,2√5)} olduğuna göre a gerçek sayısı aşağıdakilerden hangisidir?
A) -14
B) -12
C) 0
D) 12
E) 14
Cevap: A
75. a ve b sıfırdan farklı gerçek sayılar olmak üzere 3a = 4b ise a + b / 2a – b oranı kaçtır?
A) 1/2
B) 3/5
C) 5/8
D) 7/5
E) 9/4
Cevap: D
76. x/2 = 5 ve 3y – 4x = 21 ise xy değeri aşağıdakilerden hangisidir?
A) 30
B) 45
C) 60
D) 75
E) 90
Cevap: E
77. a, b ve c sıfırdan farklı gerçek sayılar olmak üzere, 2a = 3b = 5c ise a + b / b + c oranı kaçtır?
Cevap: C
78. x/y = z/t = 2/3, 2x – z + 3k = 18 ve 2y + 3m = 20 ise t sayısı kaçtır?
A) -7
B) -3
C) 10
D) 17
E) 27
Cevap: A
79. a/b = b/c = c/d = 1/4 ise d/a oranının değeri aşağıdakilerden hangisidir?
A) 1/4
B) 4
C) 1/16
D) 1/64
E) 64
Cevap: E
80. Mehmet Bey, bahçesinden topladığı 40 kg cevizi, yaşları 4, 7 ve 9 olan üç çocuğuna yaşları ile doğru orantılı olacak şekilde paylaştırıyor. Buna göre en büyük çocuk kaç ceviz almıştır?
A) 10
B) 14
C) 18
D) 22
E) 24
Cevap: C
81. Bir kurbandan 2/5 oranında kemikli et, 1/3 oranında ise kemiksiz et çıkmıştır. Bu kurbandan 20 kg kemiksiz et çıktığına göre kaç kg kemikli et çıkar?
A) 30
B) 24
C) 20
D) 18
E) 15
Cevap: B
82. Hakan, bilgisayarına bir dosya yükleme işlemi yaparken bilgisayar ekranında 750 MB olan bir dosyanın sabit hızla 630 MB nın yüklendiğini ve kalan yükleme için 4 dakika süre kaldığını görmüştür. Buna göre Hakan dosya yüklemeye kaç dakika önce başlamıştır?
A) 21
B) 25
C) 30
D) 36
E) 40
Cevap: A
83. Bir üçgenin iç açılarının ölçüleri 2,3 ve 6 ile ters orantılıdır. Buna göre bu üçgenin en küçük iç açısının ölçüsü kaç derecedir?
A) 15
B) 30
C) 45
D) 60
E) 75
Cevap: B
84. 6, 4 ve 3 sayıları ile doğru orantılı olan sayılarla ters orantılı olan sayılar aşağıdakilerden hangisinde doğru sırayla verilmiştir?
A) 1, 2, 3
B) 2, 3, 6
C) 3, 2, 1
D) 1,3, 6
E) 2, 3, 4
Cevap: E
85. a, b, c, d ve k sıfırdan farklı gerçek sayılar ve k orantı sabiti olmak üzere
• a . b = k
• b/c = k
• c = k/d
ifadeleri için aşağıdakilerden hangisi doğrudur?
A) a ile b doğru orantılıdır.
B) a ile c doğru orantılıdır.
C) b ile c ters orantılıdır.
D) b ile d doğru orantılıdır.
E) a ile d doğru orantılıdır.
Cevap: E
86. a, b, c ve k sıfırdan farklı gerçek sayılar ve k orantı sabiti olmak üzere a + b / c = b + c / a = a + c / b = k eşitliğinde k orantı sabiti aşağıdakilerden hangisidir?
A) 1
B) 2
C) 3
D) 4
E) 5
Cevap: B
87. a ve b pozitif sayıları sırasıyla 3 ile doğru, 4 ile ters orantılıdır. a . b = 48 olduğuna göre, a + b toplamı aşağıdakilerden hangisidir?
A) 14
B) 16
C) 19
D) 26
E) 49
Cevap: D
88. Bir kümesteki tavuk sayısının kaz sayısına oranı 7/2 ise kümesteki tavuk ve kaz sayıları toplamı aşağıdakilerden hangisi olabilir?
A) 66
B) 75
C) 120
D) 133
E) 144
Cevap: E
89. Müslüm’ün 4 yıl önceki yaşının 6 yıl sonraki yaşına oranı 1/3 olduğuna göre Müslüm’ün 2 yıl sonraki yaşı aşağıdakilerden hangisidir?
A) 4
B) 6
C) 8
D) 11
E) 12
Cevap: D
90. Bir sayıyı 12 den çıkardığınızda elde ettiğiniz sayının 2 katını 36 dan çıkarırsanız sonuç 18 olur. Buna göre bu sayı kaçtır?
A) 2
B) 3
C) 4
D) 6
E) 8
Cevap: B
91. Bir sepetteki elmaların -3 i yendikten sonra 8 kg daha elma yeniyor. Geriye ilk durumdaki elmaların yarısı kaldığına göre başlangıçta sepette kaç kilogram elma vardır?
A) 8
B) 24
C) 36
D) 48
E) 60
Cevap: D
92. Bir kuru yemişçideki fıstık ve fındıkların toplam ağırlığı 80 kg dır. Fıstığın kilogramı fe12, fındığın kilogramı fe48 olup bu kuru yemişlerin toplam değeri 61860 olduğuna göre kuru yemişçide kaç kilogram fındık vardır?
A) 15
B) 20
C) 25
D) 30
E) 40
Cevap: C
93. Düzenli antreman yaparak azim ve sabırla spor müsabakalarına hazırlanan Ferdi, ilk gün bir miktar yol koştuktan sonra her gün bir önceki günden 3 km fazla koşmuştur. Bir haftada toplam 77 km koştuğuna göre ilk gün kaç kilometre yol koşmuştur?
A) 1
B) 2
C) 3
D) 4
E) 5
Cevap: B
94. Bir çubuk 8 eşit parçaya ayrılıyor. Eğer bu çubuk 10 eşit parçaya ayrılsaydı parçalardan her biri 3 cm daha kısa olacaktı. Buna göre çubuğun parçalara ayrılmadan önceki boyu kaç santimetredir?
A) 80
B) 90
C) 100
D) 120
E) 160
Cevap: D
95. Aysun ve Beril’in paraları ile ilgili aşağıdakiler bilinmektedir
• Aysun, Beril’e 640 verirse paraları eşit olmaktadır.
• Beril, Aysun’a 620 verirse Aysun’un parası Beril’in parasının 5 katı olmaktadır.
Buna göre Aysun’un başlangıçtaki parası kaç Türk lirasıdır?
A) 40
B) 50
C) 80
D) 100
E) 130
Cevap: E
96. 3 litrelik ve 5 litrelik iki kovası bulunan Recep, 140 litrelik bir havuzu bu kovalarla dolduracaktır. Her kovayı tamamen doldurarak ve her kovayı en az bir kez kullanarak bu havuzu en az kaç kova suyla doldurabilir?
A) 30
B) 32
C) 38
D) 41
E) 46
Cevap: A
97. Bir sınıftaki öğrenciler bahçede üçerli sıra oluyor. Bu öğrenciler ikişerli sıra olsalardı sıra sayısı 5 artacaktı. Buna göre bu sınıfta kaç öğrenci vardır?
A) 18
B) 20
C) 24
D) 30
E) 36
Cevap: D
98. Gamze bir bilet kuyruğunda baştan (n + 1). kişi, sondan ise (2n – 3). kişidir. Kuyrukta toplam 66 kişi olduğuna göre Gamze’nin önünde kaç kişi vardır?
A) 18
B) 22
C) 23
D) 24
E) 35
Cevap: C
99. Bir telin bir ucundan bir miktar kesiliyor. Kesilen kısmın yarısı telin diğer ucuna ekleniyor. Telin orta noktası ilk duruma göre 15 cm kaydığına göre telin ucundan kaç santimetre kesilmiştir?
A) 10
B) 15
C) 20
D) 25
E) 30
Cevap: C
100. Ömer ile Fatih’in bugünkü yaşları toplamı 46 dır. Ömer’in 4 yıl önceki yaşı Fatih’in 2 yıl sonraki yaşına eşit olacağına göre Ömer’in bugünkü yaşı kaçtır?
A) 20
B) 26
C) 28
D) 30
E) 32
Cevap: B
101. AB iki basamaklı bir doğal sayı olmak üzere AB yaşındaki Osman, A + B yıl önce 2A + 2B yaşındaydı. Buna göre Osman’ın şimdiki yaşı kaçtır?
A) 18
B) 21
C) 27
D) 39
E) 48
Cevap: C
102. Nazif’in bugünkü yaşı 39 dur. Nazif, Taner’in yaşındayken Nazif’in yaşı Taner’in o günkü yaşının 2 katıydı. Buna göre Taner’in bugünkü yaşı kaçtır?
A) 34
B) 30
C) 28
D) 26
E) 21
Cevap: D
103. Bir manav bir kasa limonun kilogramını t2 ndan satarsa t28 zarar, t3 den satarsa t20 kâr etmektedir. Buna göre bir kasa limon kaç kilogramdır?
A) 28
B) 32
C) 38
D) 48
E) 58
Cevap: D
104. Selim’in çalışma odasındaki kitapların % 40 ı romandır. Romanların da %60 ı bilim kurgu romanıdır. Kitaplığında bilim kurgu türünde olmayan 152 kitabı olduğuna göre Selim’in kaç tane bilim kurgu romanı vardır?
A) 40
B) 48
C) 60
D) 96
E) 100
Cevap: B
105. Bir ürünün satış fiyatından %30 indirim yapıldığında maliyet fiyatına göre %5 kâr elde edilmektedir. Buna göre bu ürünün satış fiyatı yüzde kaç kârla belirlenmiştir?
A) 60
B) 50
C) 40
D) 35
E) 30
Cevap: B
106. k>0 olmak üzere t -3- na alınan bir mal, t -3- na satılırsa yüzde kaç kâr elde edilir?
A) 50
B) 45
C) 40
D) 30
E) 25
Cevap: E
107. Yukarıdaki tabloda bir karışımdaki malzeme miktarları ve karışım yüzdeleri verilmiştir. Buna göre x – y değeri aşağıdakilerden hangisidir?
A)1360
B) 1260
C)1040
D) 720
E) 640
Cevap: D
108. Aralarında 640 km mesafe bulunan iki şehirden hızları 70 km/sa. ve 90 km/sa. olan iki araç birbirlerine doğru aynı anda harekete başlamıştır. Bu araçlar kaç saat sonra karşılaşır?
A) 3
B) 4
C) 5
D) 6
E) 8
Cevap: B
109. Bir firmaya ait otobüs iki farklı şehir arasındaki yolu 60 km/sa. hızla gidip 90km/sa. hızla dönerek seferini tamamlamaktadır. Bu otobüsün yol boyunca ortalama hızı saatte kaç kilometre olur?
A) 84
B) 80
C) 75
D) 72
E) 64
Cevap: D
110. Yukarıdaki şekilde AC yolu asfalt, CB yolu topraktır. Asfaltta 60 km/sa., toprakta 40 km/sa. hızla hareket eden aynı türde iki kamyon aynı anda A ve B noktalarından birbirlerine doğru hareket ediyor. Bu kamyonlar kaç saat sonra karşılaşır?
A) 3
B) 3,6
C) 4
D) 4,5
E) 5
Cevap: C
111. Yukarıda verilen dikdörtgen şeklindeki pistin A noktasından hızları 3V ve 2V olan iki bisikletli aynı anda oklar yönünde hareket ederek E noktasında karşılaşıyorlar. |EC| = 20 m olduğuna göre pistin çevresi kaç metredir?
A) 120
B) 160
C) 180
D) 200
E) 240
Cevap: D
112. Yukarıdaki tabloda A+ ve A++ enerji sınıfındaki iki tür buzdolabının saatlik enerji tüketim miktarları gösterilmiştir. Ahmet Bey A++ enerji sınıfında yeni bir buzdolabı satın almıştır. 1 kW elektrik tüketim A+ enerji sınıfındaki eski buzdolabı yerine 30 gün boyunca yeni buzdolabını sürekli çalıştırmıştır. Bu durumda Ahmet Bey kaç Türk lirası tasarruf etmiştir?
A) 4,25
B) 5,08
C) 6,48
D) 8
E) 8,2
Cevap: C
113. Arda, Burak ve Canan şekildeki gibi sıralanarak “bom” oyunu oynayacaklardır. Oyunun kuralları aşağıdaki gibidir.
I) Oyuna Arda başlayacak ve şekildeki oklar yönünde ilerleyeceklerdir.
II) Arda 1 sayısını, Burak 2 sayısını, Canan 3 sayısını, Arda 4 sayısını söyledikten sonra Burak bom diyecek ve sonra Canan 6 sayısını söyleyecektir.
III) Bu şekilde devam ederek 5 in tam katlarında bom kelimesi söylenecektir. Şaşıran kişi oyunu kaybedecek ve oyun sonlanacaktır.
Bu bilgilere göre,
a) 100 sayısının yerine Arda’nın bom dediği ana kadar Burak’ın kaç kez bom dediğini bulunuz.
b) 99 sayısına gelinceye kadar Burak ile Canan’ın toplam kaç kez bom dediğini bulunuz.
c) 149 sayısına gelinceye kadar kaç kez bom denildiğini bulunuz.
Cevap:
a) 7
b) 13
c) 29
9. Sınıf Matematik Ders Kitabı Sayfa 202-203 Cevapları
1. Komşu tümler iki açının oranı 1/5 tir. Küçük açının komşu bütünlerinin ölçüsü ile büyük açının komşu bütünlerinin ölçüsü farkının kaç derece olduğunu bulunuz.
Birbirlerine oranı x e 5x diyebiliriz. Eğer bu açılar tümler açı ise
6x=90
x=15 5x=75 olarak iki açıyı buluruz.
Bütünler açılar arasındaki fark, açıların kendileri arasındaki farka eşittir. Bu durumda cevap 75-15=60
Yani cevap 60 derecedir.
2. Şekilde d1 // d2 ve d3 // d4 ise x ve y açılarının ölçülerini bulunuz.
Çözüm:
2x-10=x+70
X=80
X+70+y=180
80+70+y=180
y=50
3. Şekilde d1 // d2 ise x açısının ölçüsünü bulunuz.
Çözüm:
180-120=60
180-140=40
40+60+x=180
X=80
4. d1 // d2 ise şekilde verilenlere göre a açısının ölçüsünü bulunuz.
Noktalı açıya a, çizgili açıya b diyelim
80=a+2b
70=b+2a
150=3a+3b
a+b=50
α =2a+2b=100
5. d1 // d2 ise x açısının ölçüsünü bulunuz.
Formül= (kenar sayısı-2).180
(5-2).180=540
120+140+130=390
X=540-390=150
6. d1 // d2 ise şekilde verilenlere göre a açısının ölçüsünü bulunuz.
c=110 b=40 noktalı açı=d
c+b+2d =180
2d=30
d=15
d+α+110=180
α = 55
7. 15o< m(WA) < 65o ise A açısının tümlerinin alabileceği değer aralığını bulunuz.
A açısının tümleri onu doksana tamamlayan açıdır.
90-m(A)= m(B) dersek
25< 90-m(A) < 75
Aranan aralık ise
25< m(B) < 75
9. d1 // d2 // d3 ise şekilde verilenlere göre x + y toplamını bulunuz.
Büyük parçalardan küçük parçalara bölünme işlemi olduğu için ebob sorusudur (120,135,180)ebob=
120 135 180 | 2
60 135 90 | 2
30 135 45 | 2
15 135 45 | 3 +
5 45 15 | 3
5 15 5 | 3
5 5 5 | 5 +
1 1 1 ise EBOB(120,135,180)=15 deriz
çubuklar ayrı ayrı kesilecek ise hepsine ayrı işlem yapılmalıdır.
1. ÇUBUK (120)
120/15 = 8 8 PARÇAYI KESMEK İÇİN 7 KESİM YAPILIR
2. ÇUBUK (135)
135/15 = 9 9 PARÇAYI KESMEK İÇİN 8 KESİM YAPILIR
3. ÇUBUK (180)
180/15 = 12 12 PARÇAYI KESMEK İÇİN 11 KESİM YAPILIR
7+8+11= 26 kesim yapılır.
9. Sınıf Matematik Ders Kitabı Sayfa 218-219 Cevapları
1. Yukarıdaki her bir grup için üç doğru parçası verilmiştir.Üç doğru parçası uç uca eklendiğinde hangi grup ya da gruplarda üçgen oluştuğunu bulunuz.
2. Kenar uzunlukları tam sayı olan bir çeşitkenar üçgenin çevresinin en küçük değerini bulunuz.
Çeşitkenar üçgen demek tüm kenar uzunları birbirinden farklı olan üçgen demektir.
Ve üçgenin bir kenarı kalan iki kenarının toplamından küçük,farkından büyük olmalıdır.
Bu üçgenin kenar uzunluklarına a,b ve c diyelim.
a-c Bu değerler tamsayıdır, ve uzunluk olduğu için negatif ve sıfır olamaz.
O zaman c ye en küçük 1 değerini verebiliriz,a ya ise bundan farklı en küçük tamsayı olan 2 değerini veririz.
2-1
1
Yani a=2,b=3,c=1 çevresi en küçük =1+2+3=6 olur.
3. Yandaki şekilde verilenlere göre Ç(ABC) & nin en büyük tam sayı değerini bulunuz.

4. Yandaki şekilde verilenlere göre x in en küçük tam sayı değeri ile en büyük tam sayı değerinin toplamını bulunuz.
5. Çevresi 20 cm olan bir üçgenin bir kenar uzunluğunun tam sayı olarak en çok kaç cm olabileceğini bulunuz.
Kenar uzunluklarına a, b, c dersek:
a+b+c=20
a+b=1 olduğunu düşünürsek:
c=20-1=19 cm olacaktır.
Cevap 19'dur
6. Yandaki şekilde α > 90° olmak üzere |AC| nun alacağı sayı değerlerinin aralığını bulunuz.
Öncelikle küp oluşturmak için bütün kenarların eşit olması gerekiyor. En az dikdörtgen prizma kullanarak dediği için:
4, 5 ve 6 nın en küçük ortak katını bulmamız gerekiyor:
4 5 ve 6 'nın en küçük ortak katı 60'tır. O halde:
60/4=15
60/5=12
60/6=10
10+12+15=37 tane kullanarak bir küp oluşturabiliriz.
7. Yandaki şekilde |AC| = |AD| olmak üzere verilenlere göre |AC| nun en büyük tam sayı değerini bulunuz.
8. Yandaki şekilde BAE m(DBC) , |AE| = 7 br ve |BE| = 8 br ise |AB| nun en küçük tam sayı değerini bulunuz.
9. Yandaki şekilde D noktası ABC üçgeninin iç bölgesinde olmak üzere x in en büyük tam sayı değerini bulunuz.
10. Yukarıdaki ABC nde m(ABC) > 90° ise x in en küçük tam sayı değerinin kaç olduğunu bulunuz.
11. Yukarıdaki BAD nde m(BAD) = 90° olmak üzere
|BC| = 9 br ve |CD| = 7 br ise şekilde verilenlere göre x in en küçük tam sayı değerinin kaç olduğunu bulunuz.

9. Sınıf Matematik Ders Kitabı Sayfa 227-229 Cevapları
1. ABC , KLM ise aşağıda verilenlerin doğru olup olmadığını belirtiniz.
(D) l. |AB| = |KL|
(Y) ll. m(ACB) = m(KLM)
(D) lll. |BC| = |LM|
2. Yukarıdaki üçgenlerden ikisi eştir. Eş olan üçgenleri bularak hangi eşlik teoremine göre eş olduklarını belirtiniz.
3. Şekilde m (DAC) = m (BCA), m (DCA) = m (CAB); |AD| = (2x – 1) birim, |DC| = (3y – 2) birim, |CB| = (x + 3) birim ve |BA| = (y + 4) birim ise x + y değerini bulunuz.
4. |AD| = 7 birim ve |BC| = 6 birim olmak üzere ABC , ADC olduğuna göre |AB| + |DC| değerini bulunuz.
5. ABC ve ADE eşkenar üçgenlerdir. |AD| = 7 birim ve |BE| = 2 birim ise |DB| nu bulunuz.
6. ABC eşkenar üçgen, |BT| = |CN|, |AT| = (5 - x) br, |TN| = (x - 1) br ise x değerini bulunuz
7. Şekilde |AD| = 1 birim, |DB| = 3 birim ve |AB| = |BC| ise |DC| nu bulunuz.
8. Şekilde m(BÂC) = 25°, m(FAD) = 30° ; |AK| = |KB|, |AE| = |EF|, [DE] ⊥ [AF] ve m(ACK) = m(KCB) ise m(CAD) nü bulunuz.
9. Şekilde |AC| = | EB|, m (BDE) = m (EDO), m (AEC) = 40° ve [ DE ] = [ BC ] ise m (CBD) = a değerini bulunuz.
10. A, C, D noktaları ve E, C, B noktaları doğrusaldır. Şekilde verilenlere göre y değerini bulunuz.
11.
I. [AC] = [BD] (D)
II. |TC| > |DC| (Y)
III. |BC| = |DC| (D)
IV. |CD| > |AD| (Y)
12. Şekilde verilenlere göre yukarıdaki maddelerden hangilerinin daima doğru olduğunu bulunuz.
Şekilde verilenlere göre |AB| = | DC| = 6 birim, | AD | = | BC | = 7 birim ve I AC | = 5 birim olur.
I. [AC], BAD nın açıortayıdır.(Y)
II. m(ÂBC ) = m(CDA) tir. (D)
III. K . K . K . eşliğine göre ABC , ADC dir. (Y)
lV. [AD] // [BC] dir. (D)
Yukarıdakilerden hangisi ya da hangilerinin yanlış olduğunu bulunuz.
13. Bir ABCD dikdörtgeninde D noktası [AB] üzerindeki bir P noktasıyla çakışacak biçimde katlanıyor ve aşağıdaki şekil elde ediliyor.
I. [KL], DKP nın açıortayıdır. (D)
II. |DK| = |KP| tir. (D)
III. |DL| = | LP | tir. (D)
IV. [DP] = [KL] tir. (D)
Şekle göre yukarıdakilerden hangilerinin daima doğru olduğunu bulunuz.
9. Sınıf Matematik Ders Kitabı Sayfa 238-239 Cevapları
1. Yandaki şekilde
|AE| = 3 br, |AD| = 4 br, |BD| = 5 br ve m(ADE) = m(ACB) ise
|EC| = x değerini bulunuz.
3/9 = 4/3+x
3+x = 12
x = 9
2. Yandaki şekilde verilenlere göre aşağıdakilerden hangilerinin doğru hangilerinin yanlış olduğunu belirtiniz.
l. K . K . K . benzerlik kuralı ile ADE ~ ACB dir. (D)
ll. ACB nin ADE ne benzerlik oranı 1/2 dir. (Y 2 olmalıdır)
lll. ADE nde [AE] na ait kenarortay uzunluğunun ACB ndeki |AB| na ait kenarortay uzunluğuna oranı 1/2dir. (D)
3. Yandaki şekilde m(BAC) = m(ADC) |BC| = 3 br ve |CD| = 9 br ise |AB| nu bulunuz.
4. Yandaki şekilde [AD] // [BC],
|AD| = 3 br,
|BC| = 12 br, |AB| = 4 br ve
|BD| = 6 br ise
|DC| = x değerini bulunuz.
|BD| = 6 br ise |DC| = x değerini bulunuz.
3/6 = 6/12 = 4/x
x = 8
5. ABC~DEF olmak üzere 2 . |AB| = 3 . |DE| veriliyor. B nın açıortay uzunluğu 12 br ise E nın açıortay uzunluğu kaç br olduğunu bulunuz.
6. Yandaki şekilde m( DÂE) = m( ACB) |AD| = 6 birim ve |CD| = 4 birim ise |BC| nun kaç birim olduğunu bulunuz.
9. Sınıf Matematik Ders Kitabı Sayfa 328-330 Cevapları
1. Yandaki ABC nde [AB] ⊥ [BC] dir.
|AB| = 8 br, |BD| = 3 br ve
|AC| = 17 br olduğuna göre
A(ADC) kaç br2 olduğunu bulunuz.
2. Yandaki ABC nde [AB] ⊥ [BC] ve m(ACB) = 30° dir. |BC| = 12 br olduğuna göre A(ABC) kaç birimkare olduğunu bulunuz.
3. Yandaki ABC nde [AB] ⊥ [AC] ve m(ACB) = 15° dir. |BC| = 12 br olduğuna göre A(ABC) kaç birimkare olduğunu bulunuz.
4. Herhangi bir kenarına ait yüksekliği 4√3 br olan eşkenar üçgenin alanını bulunuz.
Kenarları ( A,B,C) alalım. Yüksekliği ise '' D '' yani (AD) = 4√ 3 daha sonraki işlemler ise ( 30-60-90 ) üçgenine göredir.
5. Yandaki ABC de |AB| = |AC|, [KT] ⊥ [AB], [TN] ⊥ [AC] ve m( BAC) = 45° dir. |KT| = 4 br ve |TN| = 2 br olduğuna göre A(ABC) kaç birimkare olduğunu bulunuz.
6. Yandaki ABC nde [AH] ⊥ [BC] ve A, T, H noktaları doğrusaldır. |AT| = 5 br ve |BC| = 12 br ise A(ABTC) kaç br2olduğunu bulunuz.


























